

A first attempt at solving this constructio problem might be to sketch a picture of what the pattern should look like. Clearly three circles are involved in creating the inner curves. The symmetro of the figure also suggests that the inner circles are congruent and the angle between their centers is 120 degrees. By rotating a radius of the circle +120 degrees and -120 degrees, we can establish a foundation for the construction. Check it out below.
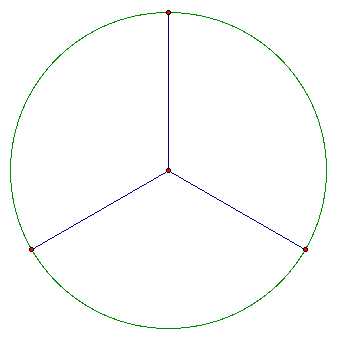
Now we can create a sort of "test circle" which will also be rotated. Using this Geometer's Sketchpad file you can drag the center of the test circle to find the (approximate) location such that the three circles are tangent. Below is a test sketch showing what this construction would look like just prior to completion. Notice that the inner circles, though very close are not actually tangent (or touching).

Recall that when two circles are tangent, their centers along with their point of intersectioni are collinear. Subsequently, points C, I, and D are collinear. Take a look at triangles CIO and DIO below. Since CI and DI are radii of congruent circles, they are congruent. Additionally, by construction, C and D are the same distance from point O meaning CO and DO are congruent. Finally, since IO is a side of both triangles, the two triangles are congruent. This means that <CIO and <DIO are congruent and necessarily each are a right angle.

A prudent next step would be to connect points that are not yet connected. In fact, it seems like connecting the centers of the inner circles might provide an interesting figure to examine.
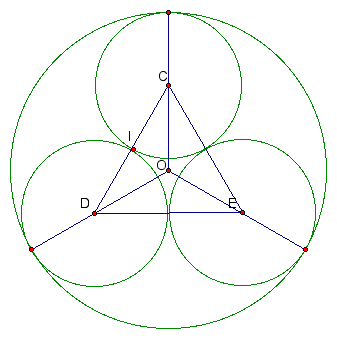
Notice that triangle COD is isosceles and has base CD and a vertex angle measuring 120 degrees. Since the base angles of any isosceles triangle are congruent, it must be the case the m<OCI = m<ODI = 30 degrees. Subseqently, in right triangle COI, the measure of angle COI must have measure 60 degrees.
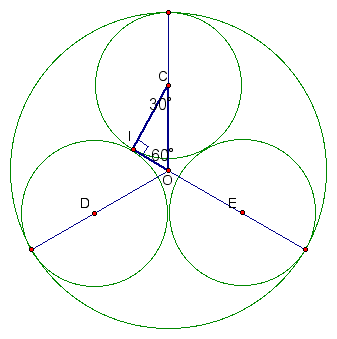
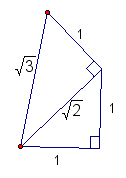
In any 30-60-90 triangle, the
side lengths are in a ratio of ![]() . If
we assume the hypotenuse of the triangle, segment CO, has length
2 we can infer that segment OI has length 1 and segment CI has
length
. If
we assume the hypotenuse of the triangle, segment CO, has length
2 we can infer that segment OI has length 1 and segment CI has
length ![]() .
.
Tah Dah! We have just found the radius of the inner circles. Very good progress . . .
Now, the task remains to figure
out how to divide a given segment into two parts, one having length
![]() and the other having length 2. It turns
out that similar triangles might be just what we need (in fact,
the technique we'll use is very similar to that used to trisect
a segment).
and the other having length 2. It turns
out that similar triangles might be just what we need (in fact,
the technique we'll use is very similar to that used to trisect
a segment).
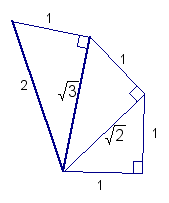
To start out, we'll need to
construct two segment whose lengths form a ![]() ratio.
We'll begin by creatin an isosceles right triangle. By creating
additional right triangles off the hypotenuse of the prevrious
one, we can construct segments of length 2 and
ratio.
We'll begin by creatin an isosceles right triangle. By creating
additional right triangles off the hypotenuse of the prevrious
one, we can construct segments of length 2 and ![]() Check
it out below.
Check
it out below.



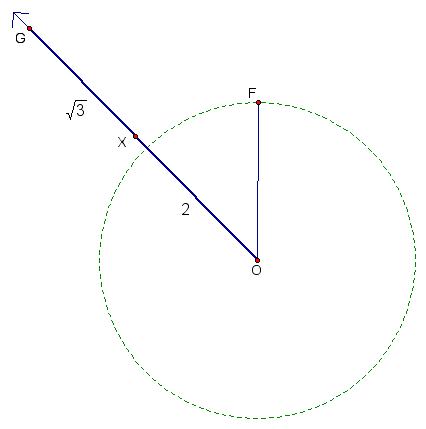
Using these segments, we've
created a ray from center O with marked segments OX having length
![]() and GX having length 2. All that remains
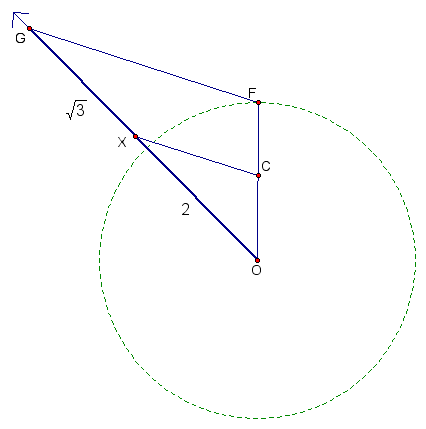
is to create the necessary similar triangles. This is accomplished
by connecting points F and G and constructing a line through X
parallel to segment FG. The intersection of that line and OF is
point C, the center of our inner circle. Check it out below.
and GX having length 2. All that remains
is to create the necessary similar triangles. This is accomplished
by connecting points F and G and constructing a line through X
parallel to segment FG. The intersection of that line and OF is
point C, the center of our inner circle. Check it out below.

Finding the centers of the other two inner circles is quite simple - just construct the circle with center O and radius OC and mark where this circle intersect the other two "foundation" lines. All that remains is to construct the inner circles and erase unnecessary lines.


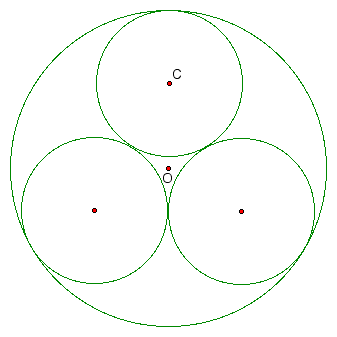

Hmmm . . . I wonder how the area of that curvy triangle in the center compares to the area of the entire circle . . .