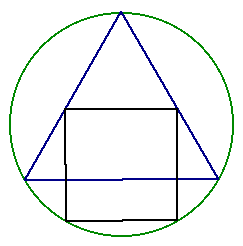
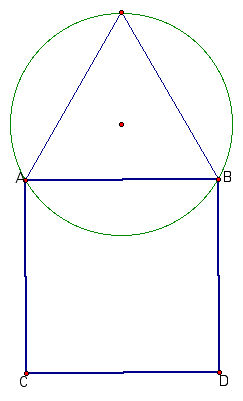
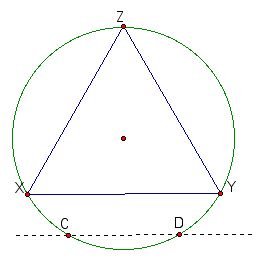
The next circle design integrates a square, equilateral triangle, and a circle. The task is as follows: Given an equilateral triangle with circumscribed circle, construct a square such that two adjacent vertices of the square lie on two sides of the equilateral triangle, and the other two vertices lie on the the circle. Additionally, two sides of the square must be parallel to one side of the triangle. In essence, we are aiming for a figure that looks something like this.

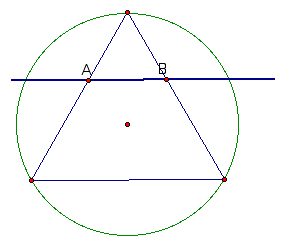
Clearly, constructing the basis of this figure, namely the equilateral triangle and circumscribed circle is a relatively simple matter. The challenge arises in determining where the vertices of the square should lie. As shown below, selecting an arbitrary location for a vertex along one side of the triangle will likely resulting in constructing a rectangle but not a square.

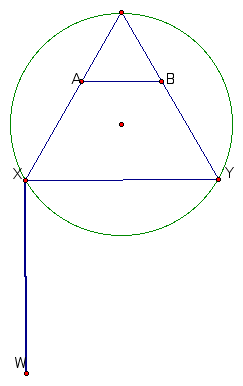
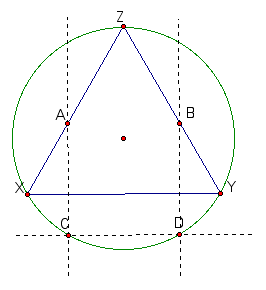
To begin finding a solution we well select a point, A, on one side of the triangle and construct B, such that AB is parallel to a side of the triangle. Now we will construct a square with side AB. Check it out below.

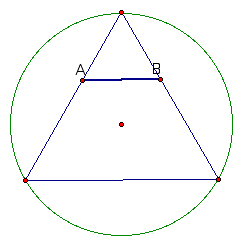
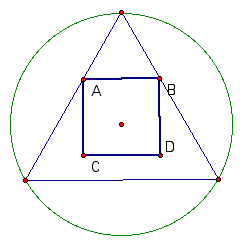
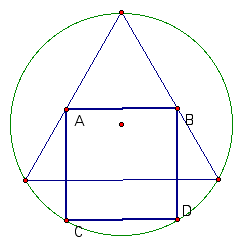
Now, the goal is to move segment AB downward until vertices C and D lie on the circle. Move vertex A in this Geometer's Sketchpad file to see how vertexd C moves as the position of AB changes. Do you notice anything interesting?

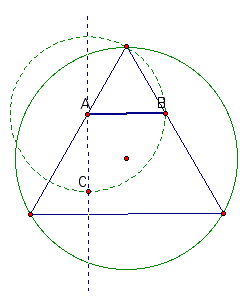
It turns out that as AB moves up or down, C moves along a straight line (you can see the path of C traced in black in the figure below). This fact will prove to be very useful for our construction . . .

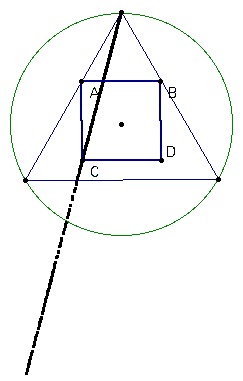
To construct the locus of C (and subsequently find the location of the vertices of the square) one must begin by looking at the extreme locations of C within our figure. As shown below, when segment AB approaches the uppermost vertex of the triangle, the length of segment AC approaches zero. This means that point C also approaches the uppermost vertex of the triangle.

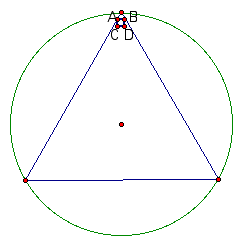
The opposite extreme situation occurrs when segment AB approaches the base of the triangle. In this situation the lenght of AB equals a side of the triangle. Since quadrilateral ABCD is a square, the length of segment AC also equals a side of the triangle. By rotating the base of the triangle by -90 degrees, we find the location of C in this extreme case. Check it out below.

By connecting these two known locations for point C we can construct the line along which this point moves as the location of AB varies.

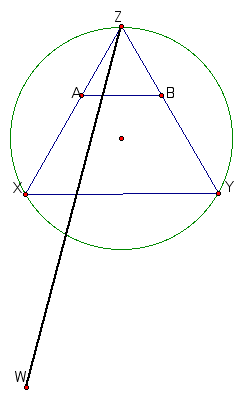
Our construction results in line segment ZW with the a much desired property. For any point on this line segment, a square having two vertices on the triangle and having two sides parallel to the base of the triangle can be constructed by drawing a line perpendicular to the base of the triangle through this point and marking its intersection with the triangle's side.

Knowing that we want two vertices of the square to also lie on the circle, we must simply choose C such that it lies on the segment ZW and on the circle. Check it out below.

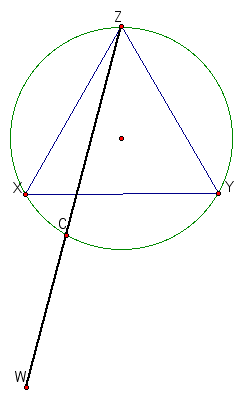
Constructing the remaining portion of the figure becomes a trivial task. Here are the results.

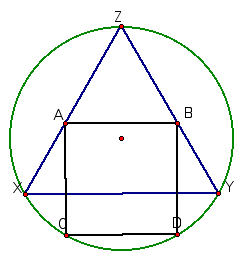
Constructing this figure is just a small piece of it's mystery. Check out some of the many peculiar properties of this figure here.