The Double Vesica (shown below) is built from the basic Vesica design.

To create the Double Vesica, we will begin with the Vesica Pisces. Construct the midpoint of the axis and the circle centered around that midpoint with diameter equal to the axis.

By erasing the dashed component of our original circles we are left with the basic structure of the Double Vesica. We must now construct the inner components of the 'eye.' It turns out that the basic structure of the inner 'eye' is based around the trisection of the original axis. Trisecting the axis will be acomplished through the use of similar triangles.

To begin, construct a line through E.

Next construct points A, B, C on the line such that AB = BC = CE (check it out below)

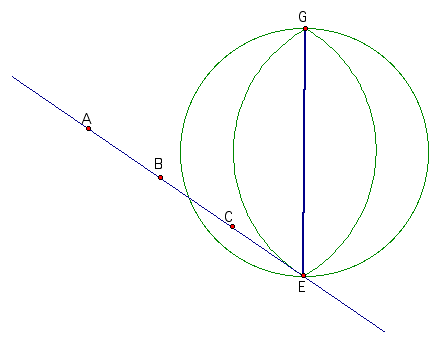
The first of our similar triangles has vertices A, G, and E.

By constructing lines parallel to AG through both B and C, three similar triangles are formed (Angle-Angle similarity).

Consequently, GF = FH = HE and we have suceeded in trisecting the axis GE.

The next series of arcs is formed by circles centered at H and F which have radius equal to 1/3 of the axis (see figure below).

Arcs XFZ and XHZ make up the inner arcs of the Double Vesica. Now all that remains is the is to construct the innermost circle of the eye (the pupil?). This turns out to be a relatively simple task. The circle must be centered about the midpoint of axis GE and tangent to arc XFZ at point F. Thus the diameter of the circle must be segement FH. Check it out below.

By erasing unnecessary lines and point we are left with the Double Vesica.

Circles having four different radii were used to construct the Double Vesica. A question arises as to what ratio exists between these radii. To examine the ration assume that the radius of the innermost circle is 1.

Consequently, the radius of the next smallest circle is 2 (notice this radius is formed by the diameter of the innermost circle.

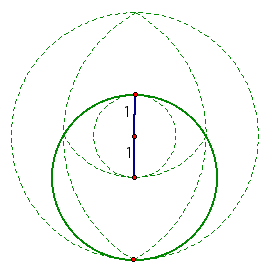
Moving outward we see that the outermost circle is has radius 3.

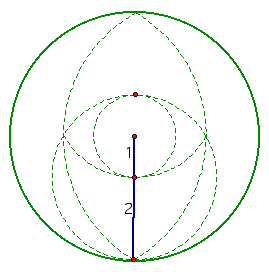
Finally, we must find the radius of the original two circles that formed the axis. We know the length of the axis is time the radius of the original circles. Thus the following is true:

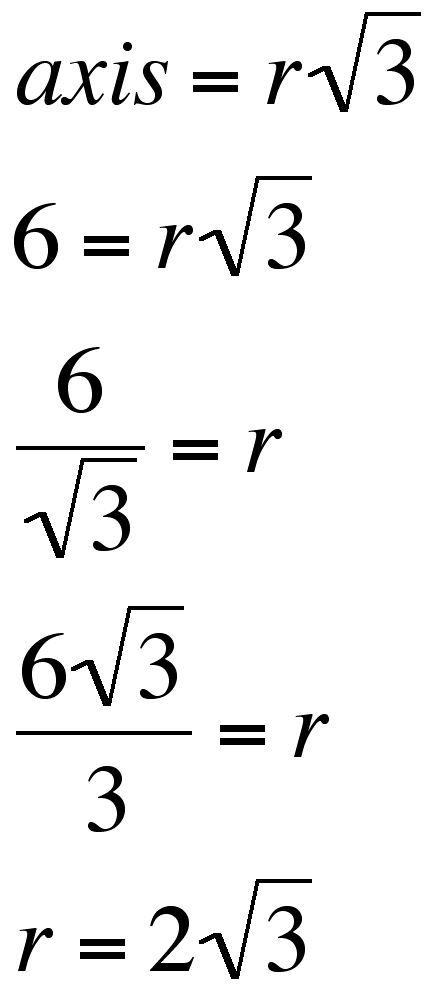
And so we find that the radii of the four circles form the following extended proportion:

After comparing radii, a natural next step would be to compare the area of these four circles. We find the following proportion for the areas:

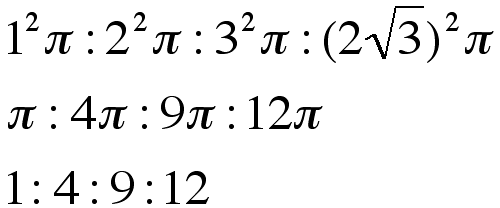
. . . a rather elegant result.