A very basic component of many crop circle designs is the vesica pisces. This figure is composed of two congruent circles, with the center of each being on the circumference of the other. It turns out that constructing this figure is fairly simply. Begin by construcing a circle and choosing a point on the circumference.

The point D will be the center of the second circle. Since the radii of the two circles are congruent, all we need to do is construct the second circle with center D that passes through C.

By constructing the intersection points of these circles, one can form an axis of the overlapping region. Check it out below.

A natural question follows: What, if any, relationship exists between the length of this axis and the radius of the circle? This Geometer's Sketchpad sketch contains our sketch as well as the measure of the radius and axis as well as a calculation of the ratio of these two segments. Spend some time changing the radius of the circles (you can either move the point "Drag Me" or clicking the "Change Radius" button). Do you notice anything interesting?

It turns out that the ratio of the axis to the radius is constant and does not change as the radius changes. Why?

To answer this question we will construct the triangle with vertices C, D, and I as shown below.

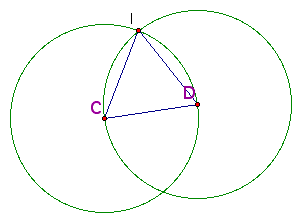
Notice that segments CI and CD are both radii of circle C. Additionally, segment ID is a radius of circle D. By construction, circles C and D are congruent thus segments CI, CD and DI are congruent. For simplicity, we will assume that the length of each of these three segments is 1.

Notice that triangle CID is an equilateral triangle; subsequently one can conclude that this triangle is equiangular (with each angle measuring 60 degrees). Next, construct the altitude of triangle CID. Since triangle CID is equilateral, this altitude is also a median of the triangle cutting segment CD into two congruent pieces. Check it out below.

Using the Pythagorean theorem one can solve for the length of segment HI as follows:

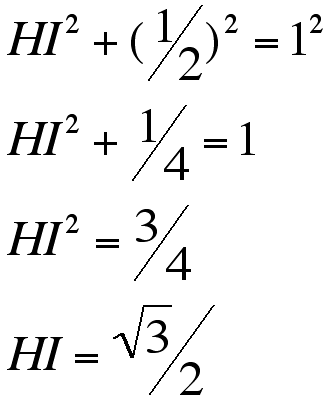
By symmetry, the distance from H to the second point of intersection will also be . Therefore the length of the axis is 2* or . So it turns out that the fixed ratio we noticed (1.73) is actually an approximation of .