Within this system of encoding patient data, a hostpital is likely to be concerned with ease of implementation. Folks typically want to keep strings of numbers which contain information, such as phone, social security, and patient numbers, to a manageable length. Thus hospital administrators may be very interested in analyzing the maximum number of digits in a patient number that will result from a given number of information slots.
Previously, we found that having 14 information slots yielded a 4 digit patient number.
However, administrators interested in the maximum length of a patient number need a more general method of determining maximum length that does not rely on computing many examples.
With the example of having 14 information slots, we see that information is encoded in the following way:
And so the maximum base 2 information number would be 1111111111111. This translates to the following patient number:
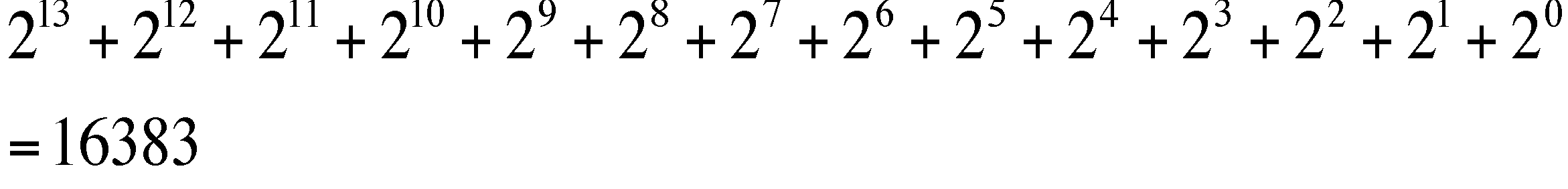
Notice that this number is necessarily one
less than 
. In general we find that the maximum patient number
for n, a given number of information slots is the following:
Using this information, hospital administrators could simply compute the largest possible patient number and count that number's digits in order to find the maximum patient number length. While this process is a bit labor intensive (computing very large powers of 2 can be tricky) it will certainly yield the desired information. But perhaps there is a simpler approach.
Examining Data
The table below offers a glimpse of
the largest possible patient number associated with a particular
number of information slots.
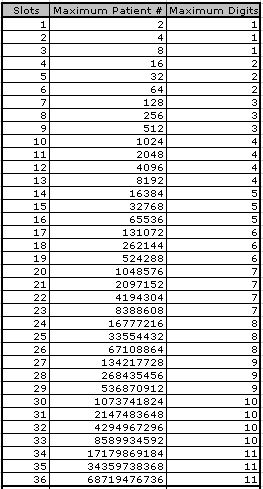
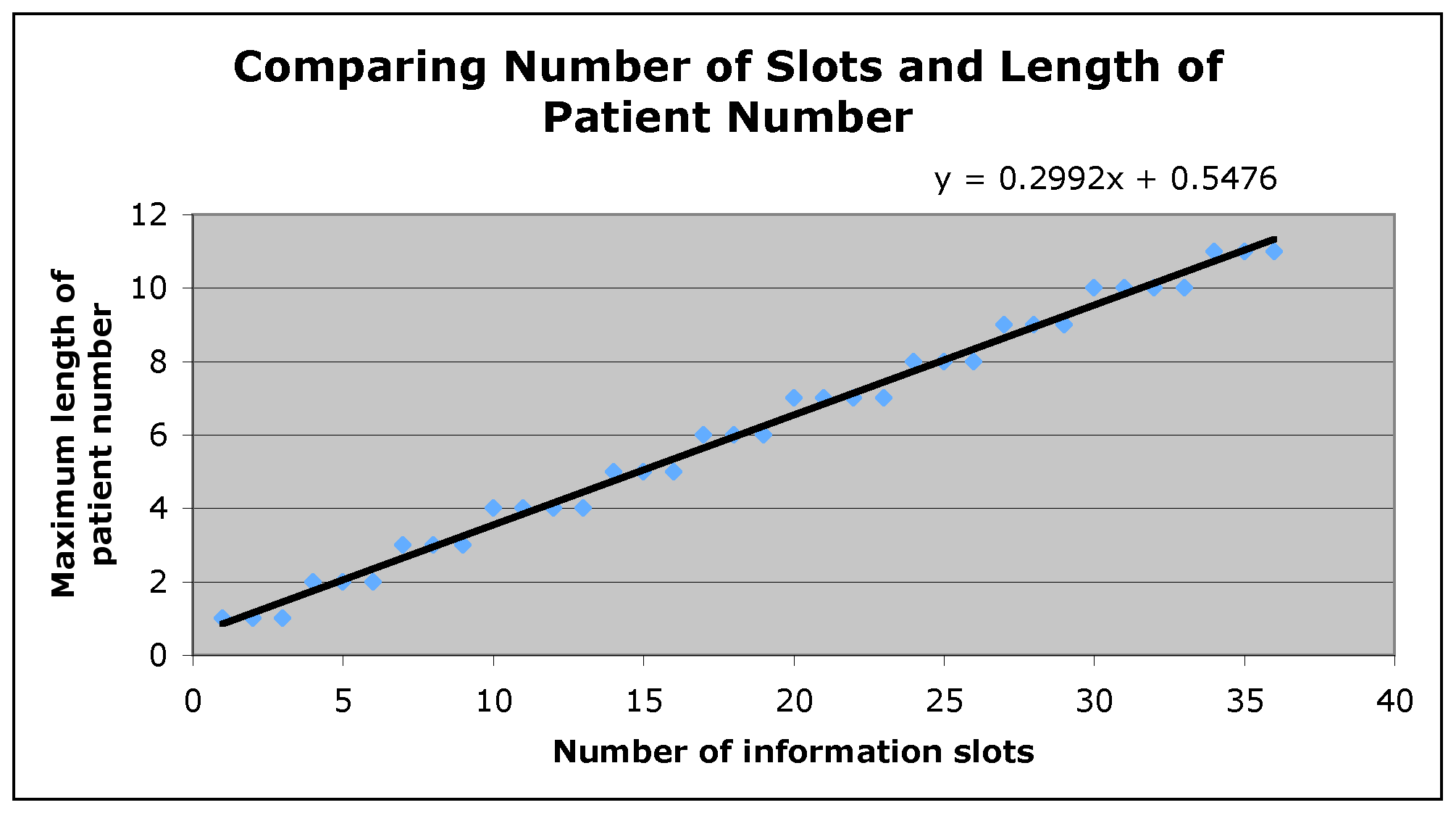
Notice that 3 different slot lengths give a patient number length of 1, 3 give a patient number of length 2, 3 give a patient number of length 3, 4 give a patient number with four digits, and so forth. By creating the following graph of the number of slots compared to the digits in the patient number, we can begin to look for patterns.
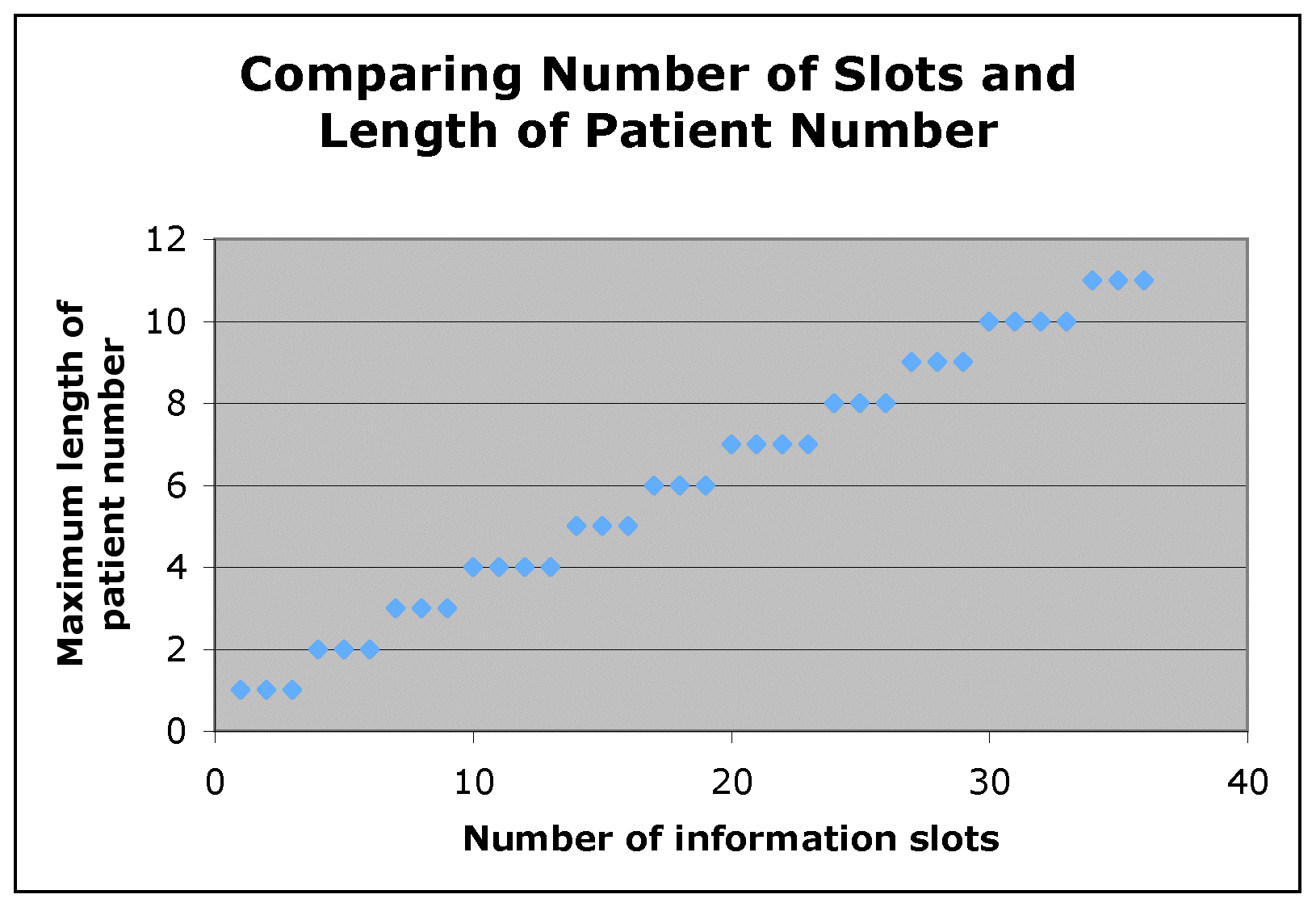
From these data, a very intersting pattern emerges. For a given 'maximum length of patient number' either three or four slot numbers result in that length. Additionally, the number of associated slot numbers seems to vary in the following pattern: 4 different slot lenghts, 3 different slot lenghts, 3 different slot lengths. If we had included data for the patient number associated with 0 slots we would locate the fourth point in the start of the pattern.
Examining the general trend in this graph we see that patient length increases roughly linearly with respect to number of slots.
It is likely that analyzing this approximately linear relationship will yield a simplified methods of approximating maximum patient number length.
Notice that each repetition of the 4-3-3 pattern accounts for 10 slots numbers. For example in the first full repetition, which we'll denote n=1, 4 different slot lenghts (10, 11, 12, 13) given maximum length 4, 3 different slot lenghts (14, 15, 16) give maximum length 5, and 3 different slot lenghts (17, 18, 19) give maximum length 6.
Therefore, one can divide the number of slots by 10 to find out in which repetition of the pattern that number of slots falls. For example, we can easily find that 36 slots falls in repetition n=3. (36/10 = 3.6 meaning three full repetitions -> n=0, n=1, and n=2 - have occurred and this repetition fall in n=3).
Notice that the sets of four occur at the following Maximum Patient Lengths: 4, 7, 10. Continuing this pattern, we see that the Maximum Patient Length for groupings of 4 equals 1+3*n where n is the repetition in which the slot number falls. Take a look at slot=31. This slot number occurs in the n=3 repetition (31/10 = 3.1). From our formula we would expect the Maximum patient length for slots=31 to be 1+3(3) = 10. This is confirmed by our data.
Similarly, we find that if the slot number falls in the first set of three within each pattern, then the maximum patient number is 2+3*n. If the slot number falls in the second set of three within each pattern, then the maximum patient number is 3+3*n.
While having to figure out whether a slot number falls in a grouping of 3 or 4 and subsequently calculating the associated Maximum Patient Length appears even more complex that computing powers of 2, noticing this pattern does help in our quest for simplicity. In fact, this pattern lets us put upper and lower bounds of the Maximum Patient Length for each slot number.
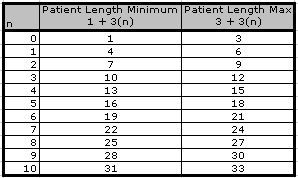
Examine slots=15. We see that this slot number falls in repetition n=1 (slots/10 = 15/10 = 1.5, so n=1). This means that the maximum patient number is greater than 3 and less than or equal to 6.
Notice the number slots/10 is between 1 and 2 and the Maximum Patient Length is between 3 and 6, or between 3(1) and 3(2). This observation implies that an approximate Maximum Patient Length can be obtained by dividing the number of slots by 10 and then multiplying that result by 3. Written more concisely, we find the following:
Let's take a look at how this approximation compares to the exact data.
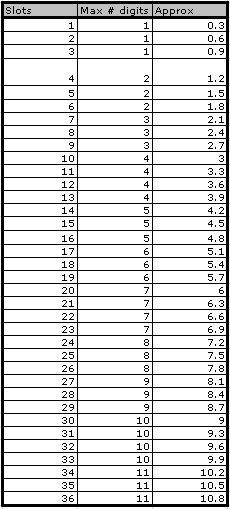
These data are very close. In fact, by rounding up every non-integer value, we obtain an every more precise approximation. Check it out below.
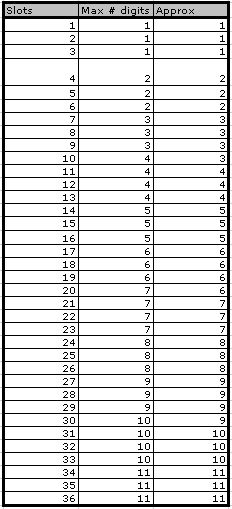
We find Maximum Patient Length is 3/10 of the number of slots, meaning that the graph of our data has a slope of approximately 3/10. By adding a linear trend line to our graph, we find confirmation in our analysis since the slope of the trendline is 0.2992 - very nearly 0.3!
