Lesson 1: Circumference of a Circle

Introduction

Student Audience:

The target audience is students studying Euclidean geometry. Anticipated completion of this lesson is 1.5 one-hour class periods.

Objectives:

§ Students will develop a general formula for the area of a regular polygon using right triangle trigonometry

§ Students will compare the perimeter of a polygon to the circumference of its inscribed circle

§ Students will compare the perimeter of a polygon to the circumference of its circumscribed circle

§ Students will graph, with the aid of technology, the perimeter of inscribed and circumscribed polygons for a given circle

§ Students will analyze the perimeter graphs to develop hypotheses about the value of the circumference of a particular circle

§ Students will develop a formula for calculating the circumference of any circle given the radius of that circle

Mathematical Concepts:

§ Perimeter of a polygon

§ Circumference of a circle

§ Right triangle trigonometry (including sine, cosine, and tangent functions)

§ Graphing functions

§ Asymptotes of a graph

§ Comparing discrete and continuous functions

§ Calculating angles of a regular polygon

Lesson Synopsis:

In a whole-class format, students will develop general formulas for finding the perimeter of any regular polygon circumscribed around a circle with a given radius. Additionally, students will develop a formula for finding the perimeter of any regular polygon inscribed in a circle with a given radius. Students will examine graphs of these formulas using Graphing Calculator software. Following a discussion of the difficulties of analyzing this situation using the graph of a continuous function, the class will develop a spreadsheet of values for these functions for integer values of n, the number of sides of the polygon. By comparing the graphs of these two discrete functions and analyzing a table of values for approximate circumference for circles of different radii, students will generate hypotheses about the relationship between the radius and circumference of any circle, leading to a formula to compute the circumference of a circle.

Lesson

Materials:

§ Classroom computer projector

§ Graphing Calculator software or similar

§ Spreadsheet software

§ Sample circumscribed/inscribed polygon spreadsheet

§ Table of Data Worksheet (optional)

Implementation:

The instructor will begin by posing the following question: Will the perimeter of a polygon that is circumscribed around a circle be larger than, smaller than, or equal to the perimeter (circumference) of the circle? Students should also form hypotheses comparing the circumference of a circle to the perimeter of any inscribed polygon.

While examining a general circumscribed polygon, students should make conjectures about how they could determine the perimeter of the polygon if they knew the radius of the circle. The instructor, in facilitating this discussion should encourage students to develop a formula for finding the perimeter of a circumscribed polygon in terms of the radius of the circle and the number of sides of the polygon. Similarly, students should develop a general formula for finding the perimeter of a polygon inscribed in a circle in terms of the radius of the circle and the number of sides the polygon has. The following formulas are likely to be developed:

Perimeter of Circumscribed Polygon

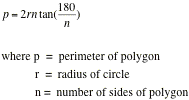
Perimeter of Inscribed Polygon

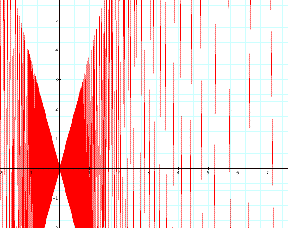
After developing these formulas, the instructor should question the students about the behavior of these two functions. Using the notion of graphs of function can help elucidate the behavior of the functions, the instructor should direct students to examine the graph of these two functions using software such as Graphing Calculator (this exploration can be done individually or whole-class). A sample file can be found here.

Inscribed “Polygon” Perimeter function

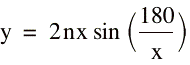
Circumscribed “Polygon” Perimeter function

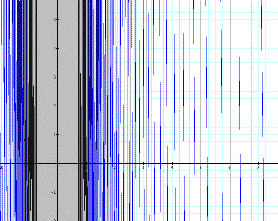
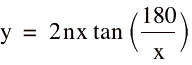
Using the facilitator questions as a guide, the instructor should probe students about the peculiar nature of these graphs. After developing the hypothesis that a graph of these functions using integer values for n (or “x”) the instructor will create or utilize the Comparison spreadsheet to calculate perimeter values for polygons having various numbers of sides that are inscribed or circumscribed around a particular circle.

After generating sample data (as shown in the sample Comparison spreadsheet), students should analyze the resulting graphs of these two functions. In particular, students should compare these graphs to the continuous function graphs previously generated. The facilitator should direct students to generate a hypothesis about the circumference of a circle in and around which these polygons have been inscribed and circumscribed? Using one particular circle and the Comparison spreadsheet data, students should generate an hypothesis for the value of the circumference of the circle.

Next, the instructor will direct students to gather data of the radius of a circle and the circumference they hypothesize that the circle will have (using the Comparison spreadsheet). This component of the lesson can be conducted individually, in small groups, or as a whole-class as technology resources permit. Student data should be compiled into a new spreadsheet. By creating a chart of the data, students can examine the relationship between the radius of a circle and the [hypothesized] circumference of the circle. A sample chart is included here.

Ultimately, students should develop a conjecture of how to estimate the circumference of a circle having any radius using the graph of their circumference/radius data. From this conjecture, the formula for the circumference of a circle may be examined.

Facilitator Questions:

§ Does the graph of the circumscribed/inscribed polygon function look like you thought it would?

§ How is the graph of this function similar to your expectations?

§ How is the graph of this function different from your expectations?

§ What do the axes of the graph represent?

§ What is the domain of each function?

§ Does the graph of each function “fit” with the mathematical situation that we are investigating (polygons with integer number of sides)?

§ How could we create a graph of these functions that more closely matches the mathematical situation we are investigating?

§ Are the continuous graph and discrete graph related?

§ How could the discrete graph be created using the continous graph?

§ How does the perimeter of the polygon change as the number of sides increases?

§ How does the perimeter of the inscribed or circumscribed polygon compare to the circumference of the circle as the number of sides is increased?

§ How does the perimeter of the inscribed n-gon compare to the perimeter of the circumscribed n-gon as the value of n gets very large?

§ What does this mean about the value of the circumference of the circle?

§ How does the estimated circumference of a circle change as the radius of the circle increases?

§ Does the relationship between the radius of a circle and the estimated circumference appear linear? Quadratic? Exponential? Something else?

§ Using your sample data points, what equation would you guess would the linear relationship that we see?

NAME __________________________________ DATE _____________

Using the table below and the Inscribed/Circumscribed Polygon comparison spreadsheet, gather and organize data about the radius and estimated circumference of circles having different radii.

Radius of Circle

Estimated Circumference of Circle