Lesson 5: Inscribed Angles
Introduction
Student Audience:
The target audience of this lesson is high school students studying Euclidean geometry. Completion of this lesson is estimated to be 1 one-hour class period.
Objectives:
á Students will investigate the meaning of the angle of an arc of a circle
á Students will deduce the method in which the angle of an arc is measured
á Students will compare the measure of an inscribed angle to the measure of its intercepted arc
á Students will discover the relationship between the measure of any inscribed angle that intercepts the same arc of a circle
á Students will prove that the measure of an inscribed angle equals half the measure of its intercepted arc.
á Students will for hypothesis about the measure of an angle inscribed in a semicircle
Mathematical Concepts:
á Arc of a circle
á Measure of central angle
á Measure of inscribed angles
á Circumscribed right triangle
á Supporting examples as compared to proof
á Counterexamples and mathematics
Lesson Synopsis:
Using a prepared GeometerŐs Sketchpad file, student will investigate the relationship between the angle of an arc of a circle and the measure of its central angle. Students will also compare inscribed angles, central angles, and intercepted arcs to deduce the relationship between the measure of an inscribed angle and the measure of its intercepted arc. Using their hypothesis as a guide, the instructor will direct a proof of their conjectures. Finally, Students will use these findings to discover the measure of any angle inscribed in a semicircle.
Lesson
Materials:
á Student access to GeometerŐs Sketchpad software
á ArcAngle.gsp GeometerŐs Sketchpad file
á InscribedAngle.gsp GeometerŐs Sketchpad file
Implementation:
The instructor will begin the lesson by introducing student to the notion of arcs of a circle. Embedded in this brief discussion will be the methods of measuring the geometric objects Đ by length and by angle measure. While measuring the length of an arc will likely prove intuitive, and understanding of the notion of the degree measure of an arc is likely to elude students. To clarify this concept, the instructor will direct students to investigate the ArcAngle.gsp file to generate hypothesis about how the angle of an arc is measured. Students may work individually, in small groups, or even collaborate as an entire class for this component of the lesson. The instructor will circulate the room, addressing points of confusion and incorporating facilitator questions as appropriate. When this portion of the lesson is complete, each student should have a firm grasp of the relationship between the measure of a central angle and the measure of its intercepted arc.
Next, students will investigate properties of inscribed angles by manipulating the figured in the InscribedAngle.gsp file. Students should complete both investigations found within this file (Investigation 1 and Investigation 2), answering associated questions within the file or on separate paper. During Investigation 1, students will manipulate the angle of an arc and observe the effect this has on the measure of the associated inscribed angle. In particular students should develop conjectures that the measure of the inscribed angle is half the measure of its intercepted arc. If students struggle to discover the 1:2 relationship between an inscribed and its intercepted arc the instructor may encourage students to collect data from their GSP file and graph this data using spreadsheet software. A sample data set and graph can be found here.
During Investigation 2, students will vary the location of the vertex of the inscribed angle (without changing the angle of the intercepted arc) and notice how the measure of the inscribed angle varies with the location of the vertex. Students should not that all angles intercepting a given arc of the circle have the same measure.
Following these investigations, the instructor will direct students to develop a proof that the measure of an inscribe angle equals half the measure of the associated central angle. Since this proof is frequently completed in multiple cases, the instructor may wish to direct all students to first examine the case where the legs of the angle are congruent. Following this proof the instructor may direct students to investigate additional cases. Alternatively, the instructor may divide students into small groups, distributing the cases among these groups. At the completion of this component of the lesson, students should have an understanding not only of this particular theorem, but also of the relationship between exploration, confirming examples, and proof.
A sample proof of one case is shown below:
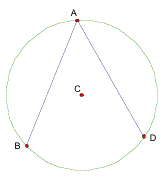 Case 1: AB is
congruent to AD
Case 1: AB is
congruent to AD
Drawing radii AC, CB, and CD we form two isosceles triangles ABC and ADC.
Since all radii are congruent and AB is congruent to AD, triangle ABC and ADC are congruent (side-side-side congruence postulate).
Since base angles of any isosceles triangle are congruent and since triangles ABC and ADC are congruent, the following angles are congruent: < CAB, <CBA, <CAD, < CDA.
Extending segment AC we form exterior angles BCE and DCE.
In any triangle, the measure of an exterior angle is twice the sum of the remote interior angles. Consequently, m<BCE = 2(m<BAC). Similarly m<DCE = 2(m< DAC). Thus m<BCD = m<BCE + m<DCE = 2(m<BAC) + 2(m<DAC) = 2(m<BAC + m<DAC) = 2(m<BAD).

Finally, students will translate their findings to answer the question of what the measure of an angle inscribe din a semicircle will be.
Facilitator Questions:
á Does
one typically measure line segment in terms of angles?
á How
is the arc of a circle like a line segment?
á How
is the arc of a circle not like a line segment?
á What
kinds of things do we measure in degrees?
á How
could we relate an angle to the arc of the circle?
á Do
you think that an inscribed angle will be larger than or smaller than an
inscribed angle?
á Do
you think an inscribed angle will be smaller than or larger than the angle of
the arc?
á What
happens to the measure of the inscribed angle as the arc becomes very large?
á What
happens to the measure of the inscribed angle as the arc becomes very small?
á What
is the smallest value that you can find for the measure of an inscribed
angle? What does the intercepted
arc look like in this situation?
á What
is the largest value you can find for the measure of an inscribed angle? What does the intercepted arc look like
in this situation?
á How
does the measure of the inscribed angle change as the location of its vertex
changes?
á Does
this change depend on whether the arc gets larger or small?
á Does
finding many positive examples ensure that a conjecture is true?
á How
can one be sure that a conjecture is true for every situation?