|
Problem 6 Cristina Aurrecoechea Fall 2005 |
We explore the following set of equations:
The following set of graphs are plotted for n = 1,2,3,4,5,6 and n = 25 (in yellow)
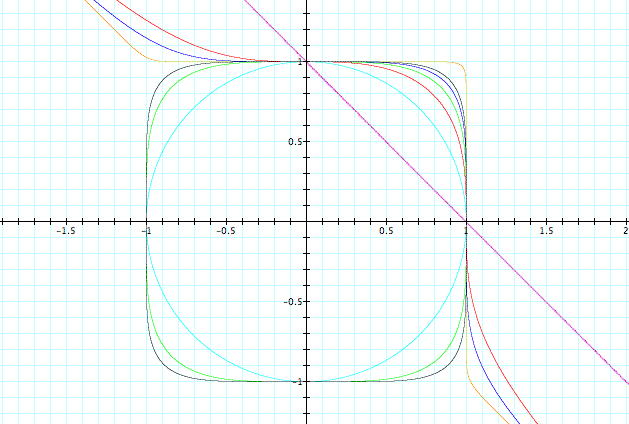
For n = 1 the equation represents a straight line x + y = 1, with negative slope.
For n = 2 the equation represents a circle centered at (0,0) and radius = 1.
Observations:
This Graphing Calculator 3.5 movie will show you the evolution from straight line, to circumference, to a pseudo-square while varying n from 1 to 15. There is a problem with the movie though. What is wrong? As n varies from 1 to 15 the line only exists in the first quadrant. But we KNOW the lines for n = 1 to 15 exist at least in 3 of the quadrants (see Figure 1 above). Why then is only the first quadrant plotted?
The problem is that, as n varies from 1 to 15, Graphing Calculator calculates the line for intermediate NON-integer values of n. (Observation: maybe the line only exists in the first quadrant for non=integer values of n? We explore that below). To solve the problem we modify the equation by introducing the ceiling() function --so n only hits integer values. This improved movie shows clearly the sequence of plotted lines for different integer values of n.
Another possible exploration is varying m
in 
. We look at how
each of the lines in this family changes, as we modify m
from 1 to larger values. We observe that as n increases
the variation introduced by higher values of m is hardly
noticeable: while for n = 1, x+y=1 is very different
from x+y=10000, for n = 25 there is hardly any difference
between m = 1 or m = 1000. Figure 2 shows the equation
for n = 25 and m = 1, 100, 10000.
(Since m does not affect the shape of the curve for a given value of n, in the following discussion we will default m to 1.)
Lets explore now 
for n = 1 to 25.
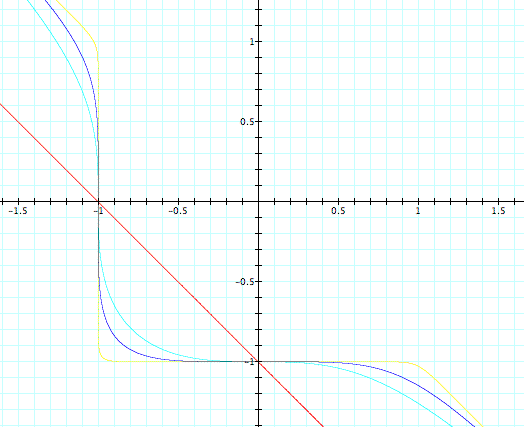
Figure 3 shows he lines that correspond to
odd values of n (1,3,5 up to 25 in yellow). For negative
m, n cannot be an even value since that would make the terms
and 
always positive and therefore their sum would never be negative.
Now lets explore negative values of n. (Let's assume m=1). For n= -1 the equation becomes:
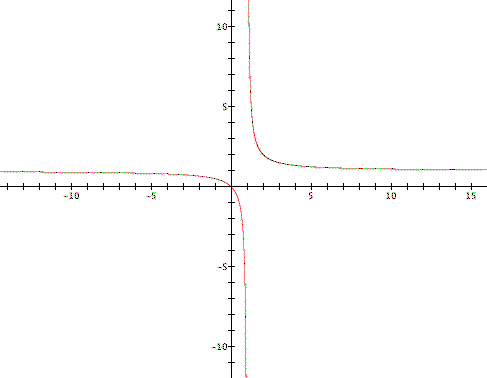
which is a rectangular hyperbola (we let you check that out). Explore for other negative values of n in the movie we have prepared.
Next, lets look at non-integer values of
n. Figure 5 shows , for
m = 4 and for n = 1, 1.5, 2 and 25. (By now
you should know which one corresponds to n = 1, n =
2, and n = 25.)
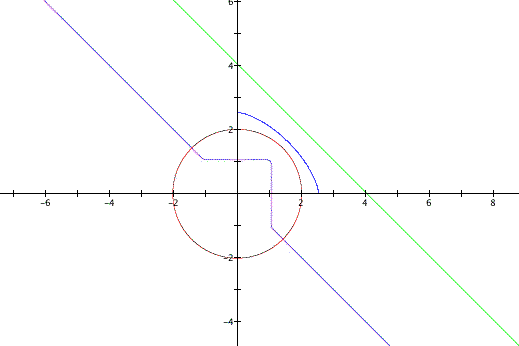
We come back to the question: Do non-integer
values of n make the line to exist only in the first quadrant?
The answer is: it depends on the rational value. For n = 1.5
we would have 
. If
there is a square root, both x and y have to be
positive for the line to exist in the real plane. On the other
hand, for n = 1/3, 
is a real number for negative values of x (e.g., for x=-8, the
result is -2).
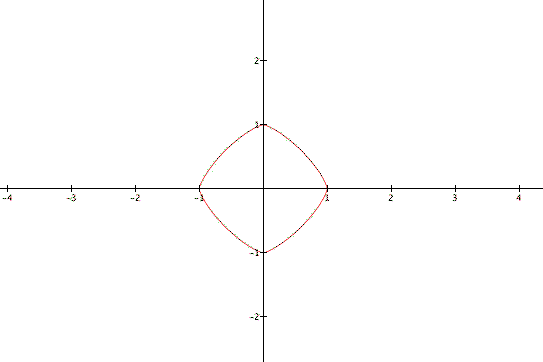
Figure 6 plots the equation for n = 4/3 and m = 1.
This movie
will show you the graph as the exponent in
varies between 1/7 and 7/2 (you can easily change those
values). (Please, do not get confused by the fact that in the
GC file we use the name "n" for the numerator in the
exponent; "n" varies between 1 and 7 while the denominator
"a" varies between 2 and 7).
It is interesting to see how the line changes from concave to convex when the exponent increases from <1 to >1. Why is the curve closed and it exists in the four quadrants for n = 4/3 and n = 2/3, while for n = 1/3 it is open and it only exists in 3 quadrants?
Finally the following gcf file will allow you to visualize all this in 3D and play with n and m values. Figure 7 is a snapshot for n = 25 and m = 1 and m = 100000; it is the 3D version of Figure 2 above.
Return to Cristina's page with all the assignments.