Assignment 10 Problem 12 Cristina Aurrecoechea Fall 2005

A cycloid is the locus of a point on a circle that rolls along a line. Here we present the parametric equations for the cycloid: we explain how to obtain the equations and graph the cycloid. Although the homework was asking for a GSP construction, we believe that our Graphic Calculator movie is just as interesting.

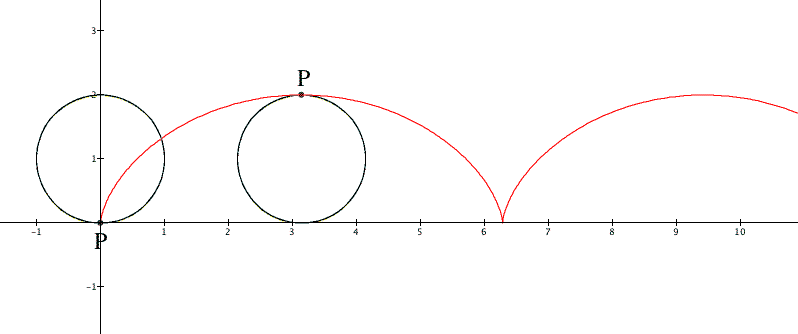
Figure 1 shows the cycloid for a rolling circle of radius a = 1. This line reflects the coordinates of a point P in the circumference of the rolling circle. This point is located at (0,0) initially, at the base of the circle. Some time later (exactly in the middle of each cycle) it will be located at the top of the circle, with a maximum y value: y = 2a; the x distance traveled by this point in each cycle is precisely the length of the circumference, which for a = 1 is .

Here you can see the equations of a rolling circle (it rolls on the x axis).

Figure 2 is a detailed snapshot of our rolling circle of radius a = 1. We will deduct the parametric equations for the cycloid based on this Figure.

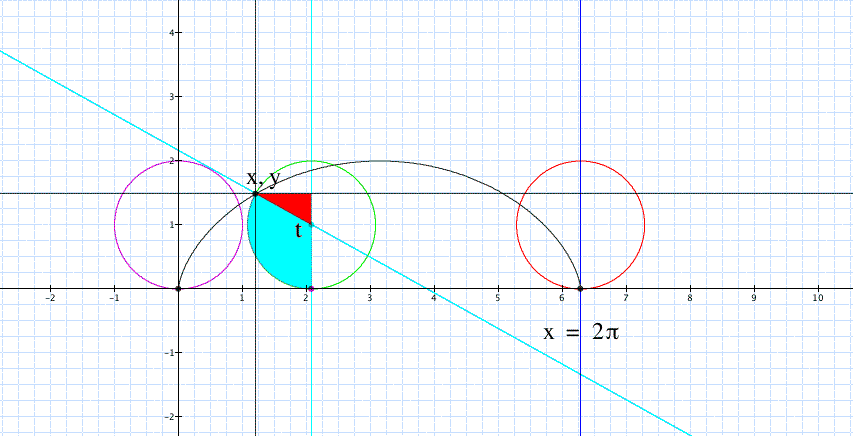
The rolling circle at time zero is shown in purple. We look at the coordinates (x,y) of the point at its base located initially at coordinates (0,0). As the circle rolls we follow the trace of this point (x,y) up to the position shown in the green circle. At this point the circle has rotated t radians. The angle t and its arc are shown by shading the area in light blue. The arc is equal to the product ( angle * radius ); in general for a radius a the arc is at.

Lets calculate the coordinates (x,y) of our point as a function of the angle t. That will give us the parametric equations for the cycloid. Our calculations will be based on the red triangle.

x is the rolled arc (at) minus the horizontal side of the red triangle, which is a.sin (-t). Therefore given that sin(-t) = sin(t) we have:

y is the radius a plus the vertical side of the red triangle, which is a.cos(-t). Therefore given that cos(-t) = -cos(t), we have:

Next we have a set of movies for you to play with the cycloid function and rolling circle:

• cycloid: slider n allows you to control the number of cycles; the slider a modifies the radius.
• rolling circle, radius = 1, one cycle (360 degrees): here
• rolling circle, radius = 1, three cycles (t=about 20 radians): here
• rolling circle, radius = a, a is provided as a slider: here

Return to Cristina's page with all the assignments.