Assignment 9 Pedal Triangles (1,4 to 11) Cristina Aurrecoechea Fall 2005

Given a triangle and a point P (the Pedal), the Pedal Triangle has as vertices the intersection points of the perpendicular lines from P to the sides of the triangle (or extending lines). From the definition it follows that the medial triangle is the pedal triangle when P is C the circumcenter and the orthic triangle is the pedal triangle when P is H the orthocenter.

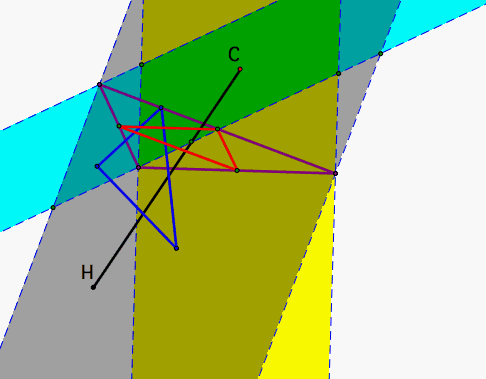
Figure 1 shows the pedal triangle as P is located inside or outside of an acute or an obtuse triangle. If the triangle is acute it seems that if P is inside, the pedal triangle is also inside. But if the triangle is obtuse, it does not work that way.

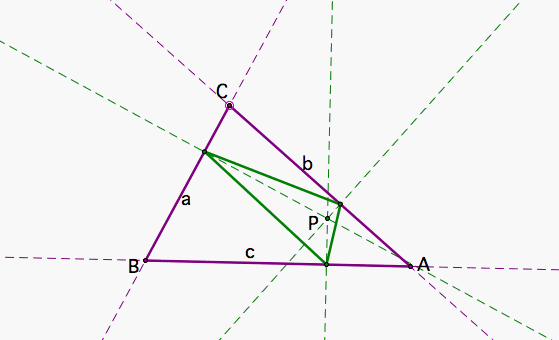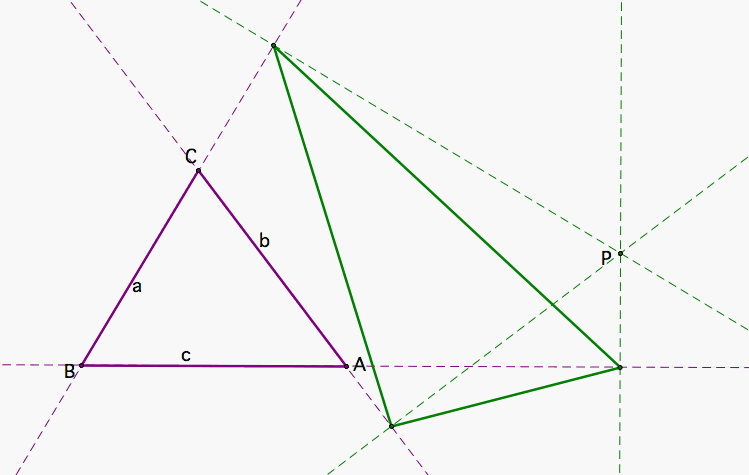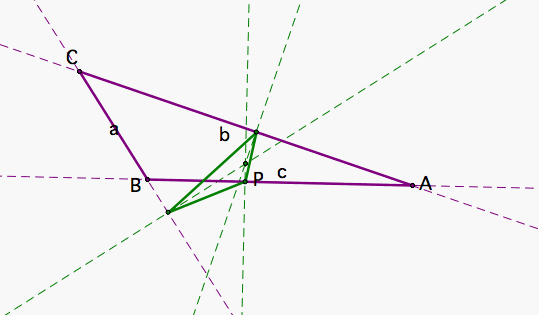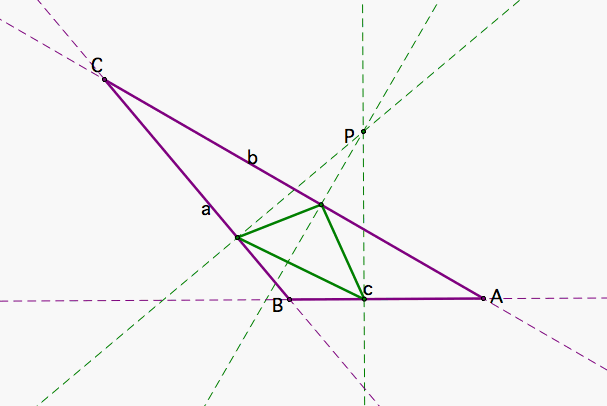From the definition we know that the vertices of the pedal triangle are always on the sides of the triangle or on the sides' extended lines. We have prepared a gsp file that helps in visualizing the different sections where P can be located, so the vertices of the pedal triangle are on the side or external to the side, for different shapes of the original triangle. Figure 2 is a snapshot of this file. The colored regions are generated by tracing perpendicular lines to the sides of the triangle.

There are four types of regions:

• White region. If P is in the white region, as shown in Figure 2, the three vertices are external to the sides and the pedal triangle does not intersect with the original triangle.
• Yellow, Blue or Grey regions (single colors). The pedal triangle has only one vertex on a side of the original triangle; the other two vertices ae external to the sides.
• Light green, Dark blue or Dark yellow (combining two colors). The pedal triangle has two vertices on the sides of the original triangle.
• Dark green region (combinig the three colors yellow, blue and gray). If P is located in this region the pedal triangle is internal to the original triangle, the three vertices stay on the sides.

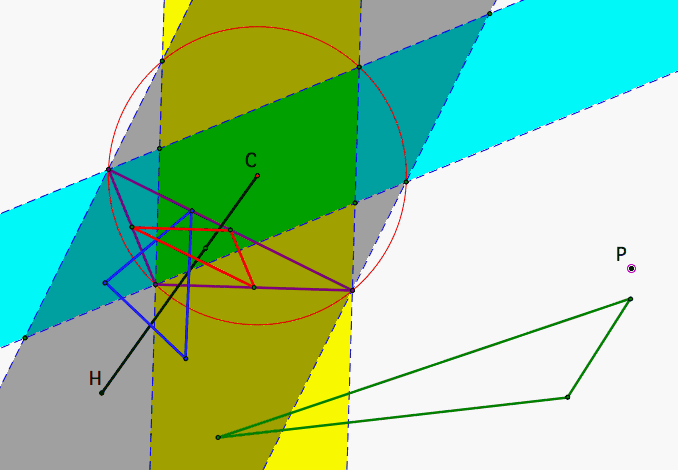
From all that has been said, it follows that the circumcenter will always stay inside the Dark Green area, since the medial triangle always stays inside the triangle. The orthocenter will move through different regions: Dark Green area or single color area (Yellow, Grey or Blue) but never in the White area or in two color combinations. Figure 3 shows a snapshot with C and H for an obtuse triangle. Use this file to explore this assertions.

Questions 6,7 and 8 in the Assignment: How is the Pedal Triangle if ...? To answer them we use these colored regions and look at Figures 2 and 3 for when the original triangle is acute or obtuse, respectively. (You can use the tool provided here to construct the center of the nine point circle, though we know N (the center of the nine-point circle) lies in the midpoint of the euler line.)

In the case of acute triangle, we know that if P is on the sides of the triangle, it is in the Dark Green region, so the pedal triangle will be inside the original triangle, that is, the three vertices will lie on the sides of the original triangle. If P is on the vertices the pedal triangle degenerates into a segment (the Simson Line). In an acute triangle this line is inside the triangle and intersects on the opposite side to P. Finally, if P is N, if the triangle is acute, N lies inside the triangle therefore the pedal triangle will too.

In the case of an obtuse triangle it is more difficult to say exactly what will happen. Different things can happen. If P is N, we know C will always be in the Dark Green area while H will never be in the White area, nor in the double color areas, so N could be in any of the color combinations but never in the White. Therefore the pedal triangle, if P is N, could have three, two or only one vertex on the side of the original triangle.

Pedal located on a circle concentric to the circumcircle

How is the Pedal Triangle as P moves along a circle that is concentric to the circumcircle? Or on the circumcircle? Expore with this file. We see that when P is on the circumcircle the Pedal Triangle degenerates into a segment: the Simson Line. This segment can be inside the triangle, touching two sides or no side, depending on the shape of the triangle.

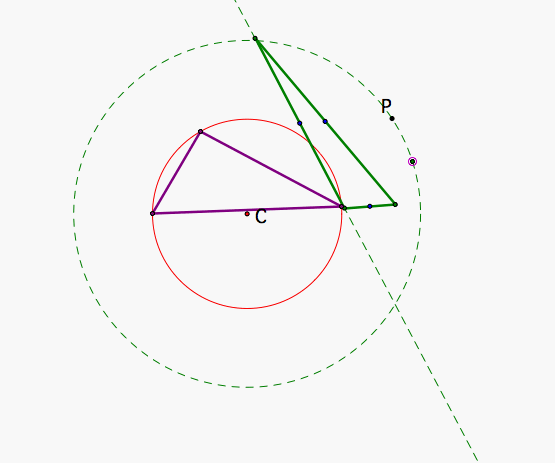
It could help looking at how the circumcircle falls in the regions. In Figure 5 we see that for the case of an obtuse triangle the circumcircle does lie on some white areas therefore the Simson Line will be detached from the triangle when P is on these two arcs. It is also interesting to notice that the circumcicle passes through the intersections between regions.

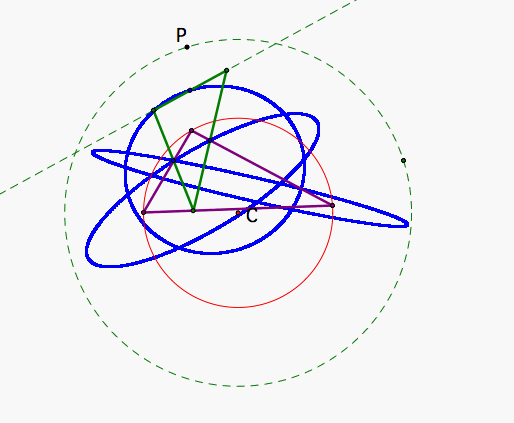
This file traces the midpoints of the sides of the Pedal Triangle, whose locus are ellipses. Figure 6 is a snapshot that shows the ellipses in blue.

This file traces the line that extends a side of the Pedal Triangle. Figure 7 is a snapshot when P is on the circumcircle.

Given an original triangle ABC, the pedal of pedal of pedal of the original is similar to the original triangle

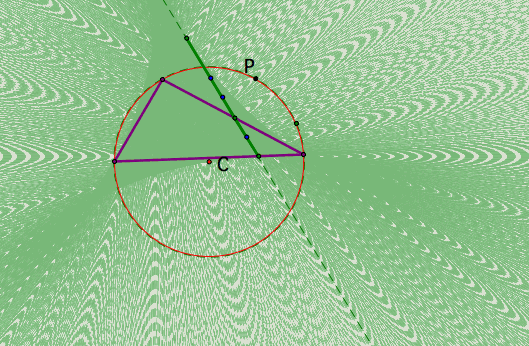
Figure 8 shows a snapshot from this file that you can use to explore this fact.

Return to Cristina's page with all the assignments.