

|
Cristina Aurrecoechea Fall 2005 |
Barney is in a triangular room. His path is always parallel in turn to each side of the triangle. Prove that Barney will eventually return to his starting point. How many times will he reach a wall before returning to his starting point? Discuss for various starting points including points exterior to triangle segments.
We generated the construction in this file. As shown in Figure 1, independently on where he starts, Barney does always return to his starting point after two rounds (after hitting each wall twice). The triangles generated in Figure 1 are similar to the original.
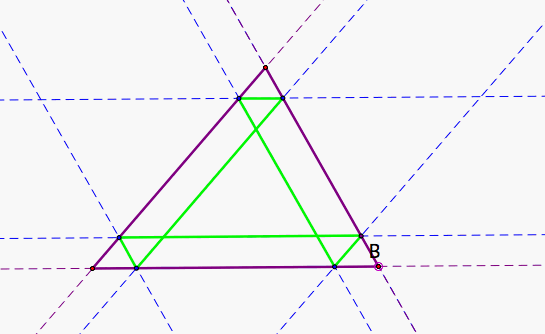
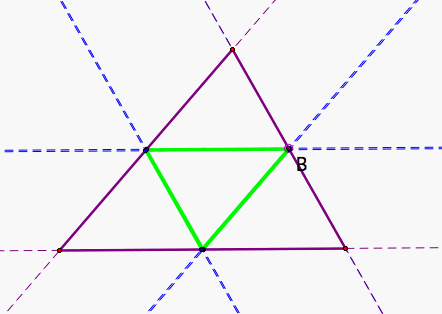
The only exception to this is when he starts in the middle of a side, then it only hits each wall once. This is the medial triangle, shown in Figure 2.
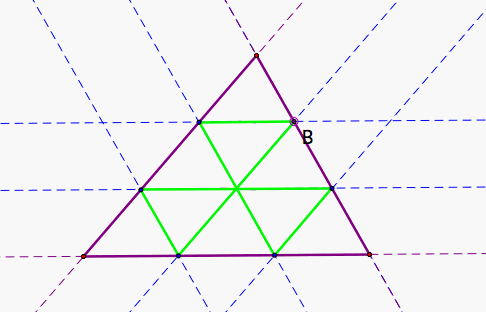
When Barney starts at a third of a side, nine congruent triangles are generated, shown in Figure 3, all similar to the original triangle.
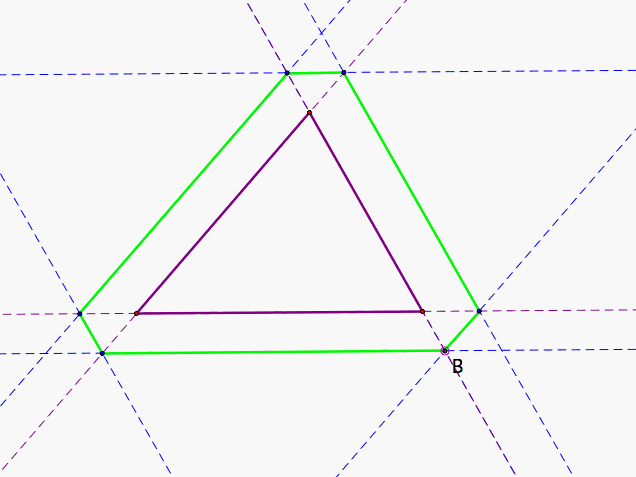
If Barney starts outside, he stays outside. Figure 4 shows its path.
Return to Cristina's page with all the assignments.