Final Assignment Cristina Aurrecoechea Fall 2005

Multiple Solutions

Find as many solutions as possible for x,y,z that satisfy the equations:

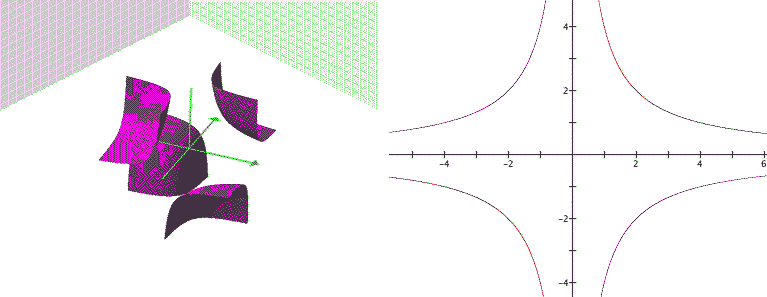
First let's look at these surfaces in 3D. The first one is a hyperboloid shown in Figure 1. We observe the following about this surface:

• It does not intersect any of the three axes x=0, y=0, z=0, in any point.
• It only exists in 4 quadrants: For z > 0, the product xy must be positive, therefore the curve will exist in the first and third quadrant only.
• For z < 0, the product xy must be negative, therefore the curve will exist in the sixth and fourth eighth quadrants.

The right side of Figure 1 shows the projection in plane z = 0 of the intersection between the hyperboloid and z = 1 (in red, quadrants 1 and 3) and z = -1 (in blue, quadrants 2 and 4).

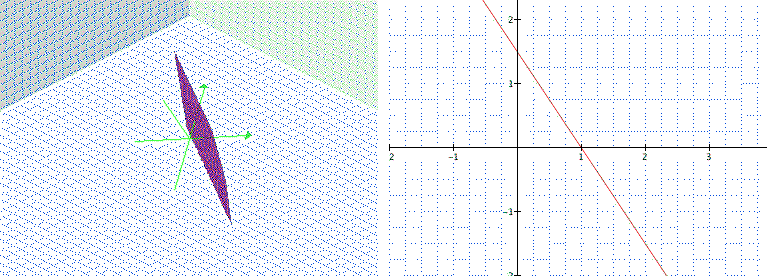
The second equation is a plane in 3D as shown in Figure 2. The right side shows the intersection of the plane with z=0 (a straight line). The plane will intersect the z axis (x=0, y=0) for z=-3 (unfortunately the 3D Figure 2 does not show the z axis for z < 0.)

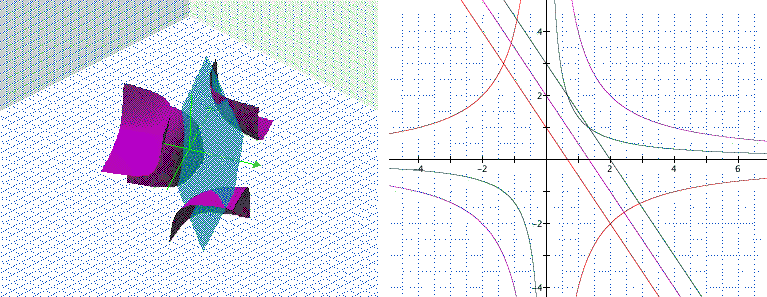
The intersection of both surfaces is a curved line. Figure 3 shows the intersection in 3D. The right side of Figure 3 shows the projection on plane z = 0 of the intersection between the two surfaces with z = -1 (red), z = 1 (purple) and z=3 (black). In z = - 1 there are two intersecting points (for any z < 0), each in quadrants second (sixth) and fourth (eighth) ; for z = 1 there is no intersection between both surfaces (the resulting curve does not exist for z = 1). Finally for z = 3 there are again two intersection points, both in quadrant first.

So we have concluded that the resulting curve if projected into the xy plane, it exists in the first, second and fourth quadrants.

Given the two equations above, if we obtain z in the first equation and substitute z in the second equation, we obtain the following equation that is graphed in Figure 4:

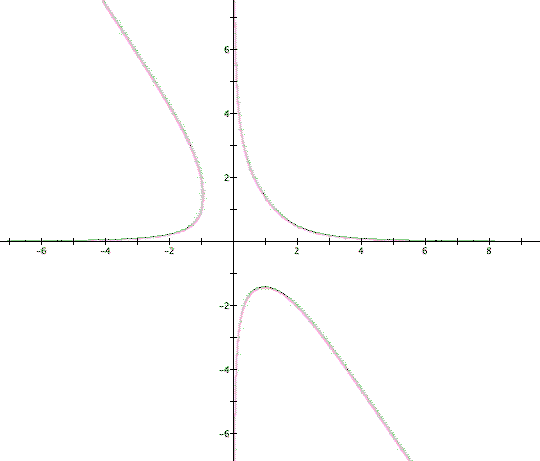
To obtain multiple x,y,z solutions, we can give a value to z, for example z = -1; that gives us two equations with two unknowns x and y:

if we have x = -4/y, substituting in the second equation gives us a quadratic equation on y:

that gives us y = 3 and y = -2. For those values, x = -4/3 and x=2 respectively. Therefore two solutions are: (-4/3, 3, -1) and (2, -2, -1). We can repeat this process for any negative value of z and we will obtain 2 points for each z value. We can also repeat this process for any positive z value > 3 and we will have again two points for each z value.

An excel sheet would give us fast a set of values. Tables 1 and 2 are snapshots of the excel sheet (I dont know why the cell format --3 decimal digits-- did not stay).

Create another set of equations that also yield a useful exploration.

This is another set of equations that represent two surfaces intersecting.

Figure 5 shows the resulting curve in 3D.

Return to Cristina's page with all the assignments.