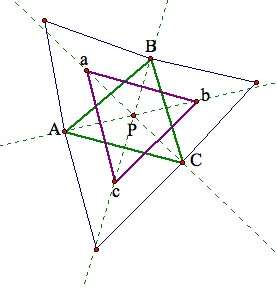
Napoleon's Triangle
by
Nikki Bacon
Given any triangle ABC, construct equilateral triangles on each side and find the center of each equilateral triangle. The triangle formed by these three centers is Napoleon's Triangle (yellow triangle).
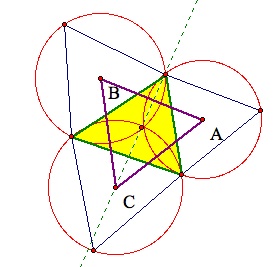
The figure above shows the Outer Napoleon Triangle. If you construct equilateral triangles on the interior of each side of the triangle and find the center of each equilateral triangle, the triangle that forms from the three centers is the Inner Napolean Triangle (yellow triangle). To see a construction, click here.
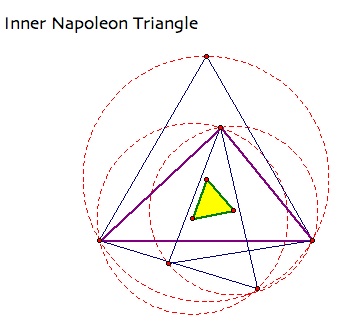
Napoleon's Triangle is also an equilateral triangle. To see a proof, click here.
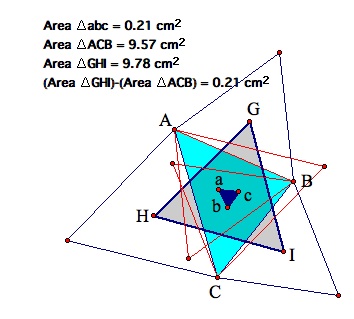
Also, the area of the outer Napoleon Triangle (Triangle GHI) minus the area of the inner Napoleon Triangle (Triangle abc) is equal to the area of the original triangle (Triangle ABC).
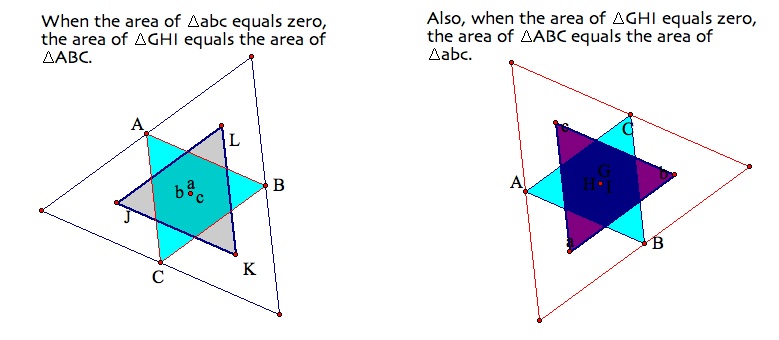
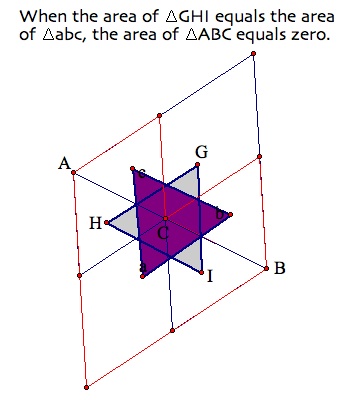
By consructing segments from the verticies of the original triangle to the opposite vertice of Napolean's triangle, you construct Fermat's point. Fermat's point is unique and lies on the intersection of the three straight lines.
To read more about Fermat's point, click here