Hohmann Transfers

A Hohmann Transfer is an orbital maneuver that transfers a satellite or spacecraft from one circular orbit to another. It was invented by a German scientist in 1925 and is the most fuel efficient way to get from one circular orbit to another circular orbit. Because the Hohmann Transfer is the most fuel efficient way to move a spacecraft, it is a fairly slow process and is used mostly for transferring spacecraft shorter distances.

A Hohmann Transfer is half of an elliptical orbit (2) that touches the circular orbit the spacecraft is currently on (1) and the circular orbit the spacecraft will end up on (3). It takes two accelerations to get the original orbit to the destination orbit. To move from a smaller circular orbit to a larger one the spacecraft will need to speed up to get onto the elliptical orbit at the perigee and speed up again at the apogee to get onto the new circular orbit. To move from a larger circluar orbit to a smaller one, the processes are reversed.

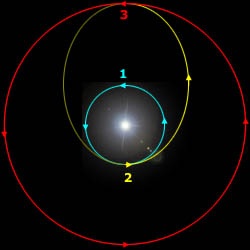
Day 1

In order to understand the Hohmann Transfer, students must first know a little about orbits. The Hohmann Transfer consists of two circular orbits and one elliptical orbit.

For circular orbits students should know:

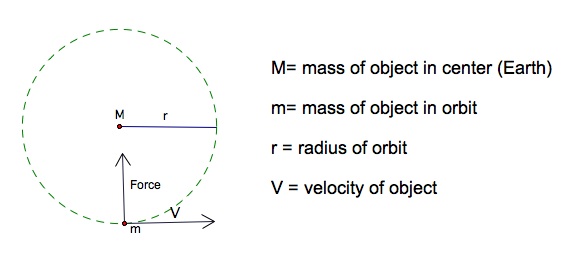
Discuss the radius of the orbit with students. Is the radius constant or does it change and why?

Students need to understand the difference between speed and velocity.

Speed is a scalar quantity which refers to "how fast an object is moving." A fast-moving object has a highspeed while a slow-moving object has a low speed. An object with no movement at all has a zero speed.
Velocity is a vector quantity which refers to "the rate at which an object changes its position." Imagine a person moving rapidly - one step forward and one step back - always returning to the original starting position. While this might result in a frenzy of activity, it would result in a zero velocity.

* Speed is a scalar and does not keep track of direction; velocity is a vector and is direction-aware.

There are two types of forces involved in orbits. F1 is the force that pushes down on the Earth (in this case) from the other object and F2 is the force between two objects in general.

We define F1 and F2 as:

Discuss with students the speed of an object in a circular orbit (constant because the radius is constant) and the force of an object (also constant). F2 always equals a constant and is always equal to F1.

Now that students know this information, they can calculate the velocity of an object in a circular orbit.

Let F1 = F2 and solve for V. We get,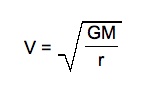

Also, discuss the inverse relationship between the radius of the circular orbit and the velocity of the object. Ask them what happens to the velocity as the radius increases and when it decreases.

For student note sheet on Day 1, click here.

Day 2

For elliptical orbits students should know:

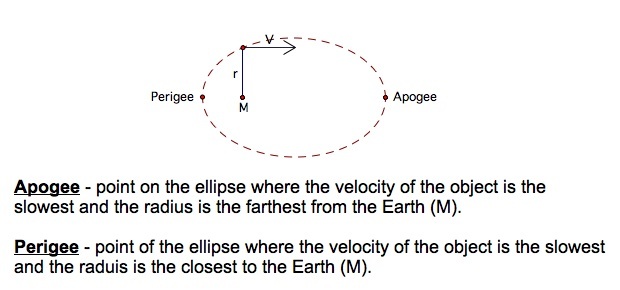
Again, disucss with the students the speed of an object in an elliptical orbit. The speed is not constant because the radius changes. When the radius is the greatest, at the Apogee, velocity will be at the minmum. When the radius is the smallest, at the Perigee, velocity is at the maximum.

All that is left is to find the velocity of an object in an elliptical orbit. This is where it gets a little tricky.

*** Teacher's, from this point on use your discretion on how much information you want to give your studnets. How much you lead them will depend on the level of your students.

In order to find the velocity, students need to have a basic understanding of kinetic energy and potential energy. Potential energy is stored energy, while kinetic energy is energy of motion. It is the energy it possesses because of its motion. If we subtract an objects potential energy from its kinetic energy, we get the total amount of energy an object possesses. We know the formula for the potential energy, kinetic energy and the total energy of an object, so we can substitute those into the formula and solve for velocity.

To simplify things, substitute 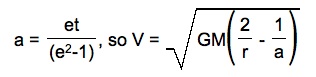, where a is half the distance of the major axis or the distance from one vertex to the center.

For student note sheet on Day 2, click here.

Day 3

Now we know how to find the velocity of an object in a circular orbit and an elliptical orbit. Ask students what else they think they need to know to successfully make a Hohmann Transfer. Talk a little more about what it is and how it is done to lead them to the conclusion that they also need to know the velocity at the apogee and perigee in order to transfer the spacecraft from one orbit to the next.

In order to find the velocity at the apogee and perigee, it is important that students understand the eccentricity of ellipses and how to label a and c on an ellipse. Have students refer to the diagram below.

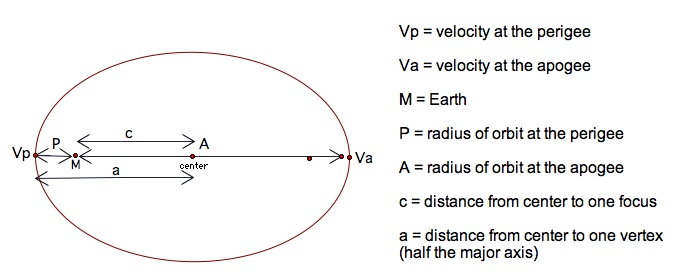
We already know that the velocity of an object in a elliptical orbit is

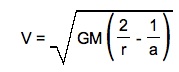
In order to find the velocity at A and P, we need to put the formula in terms of A and P. This is where eccentricity and our diagram come into play.

Talk about whether velocity is faster at the apogee or perigee. Students should come to the conclusion that Vp > Va because the radius is the shortest at the perigee, which means velocity is at its fastest.

Now that students can find the velocity of an object in a circular and elliptical orbit, and the velocity of an object at the apogee and perigee of an elliptical orbit, they can begin to explain how to move a spacecraft from one circular orbit to another.

For student note sheet on Day 3, click here.

Day 4

The following worksheet , adapted from Andrew Izsak's EMAT 6550 course on conic sections at UGA, will lead them in performing a Hohmann Transfer.

Click here for an answer sheet.

Back to my homepage