This activity leads you through some
investigations of the polar equation 
Start with the
equation .
Let's begin our investigation by observing what the function of this
equation looks like for different values of a, b, and k respectively
while holding the other two values constant.
Let r = a + cos
(2ø). The following graph shows what happens when a = -3,
-2, -1, 0, 1, 2, 3.
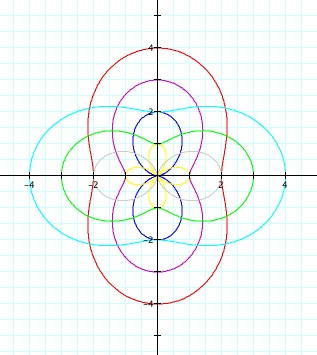
Notice that when a
< 0, the graph is stretched in the vertical direction, along the y
axis. Also,
notice when a < -1, the curve intersects the x axis at |a| - 1 and
the y axis at |a| +1. When a > 0, the graph is
stretched in the horizontal direction, along the x axis. When a >1, the curve
intersects the y axis at |a| - 1 and the x axis at |a| +1. These graphs are
all centered on the origin. Notice also, that when |a| is less
than or equal to 1, the graph of the curve intersects the origin.
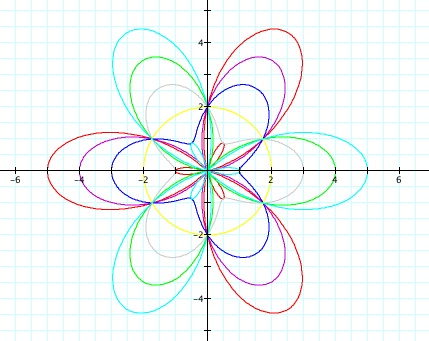
When b = 0, the graph is a
circle. When b does not equal 0, the graph has three
leaves. When b is negative the graph is symmetric about the
line y = x. When b is positive, the graph is symmetric about the
line y = -x.
Compare this to the graph of the equation, r = b cos (3ø), where
a = 0.
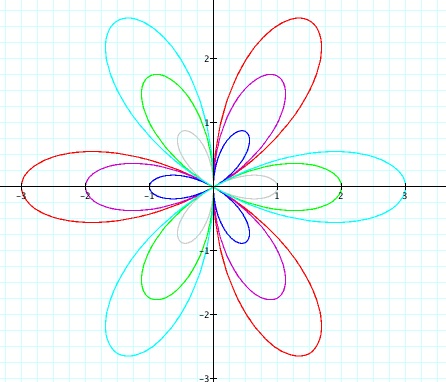
The same properties of symmetry still apply from the previous
example. This graph is a bit more simplistic then the last
graph in that each equation only has one set of leaves. Looking
back at the previous picture, several of the equations have two sets of
similar leaves.
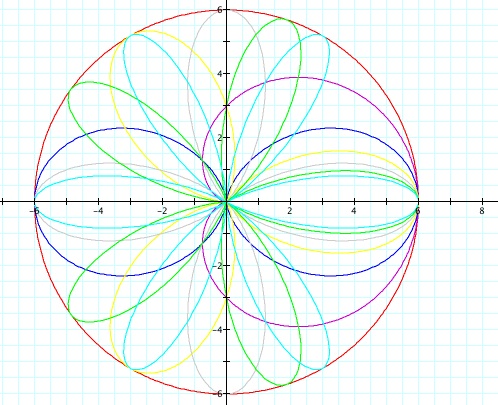
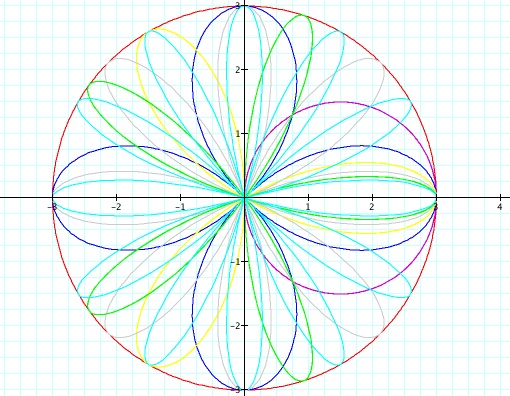
Notice when k = 0 and k = 1, the graph is a circle. When k >
1, the graph is an n-leaf rose. Again, when k is even, the graph
of the equation is centered on the x axis.