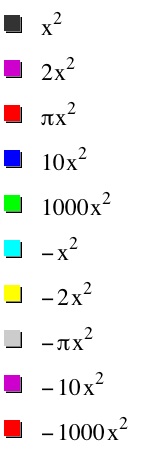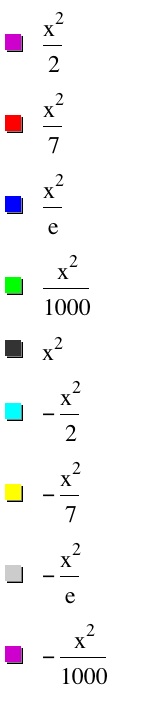Assignment 2
This exploration examines the graph of y = ax² for
different
values of a.
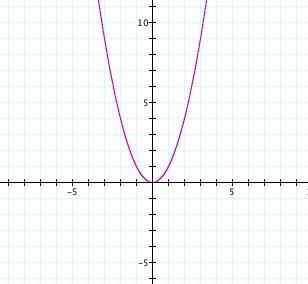
Start with the
function y = x².
First observe what happens to this
function when a > 1.
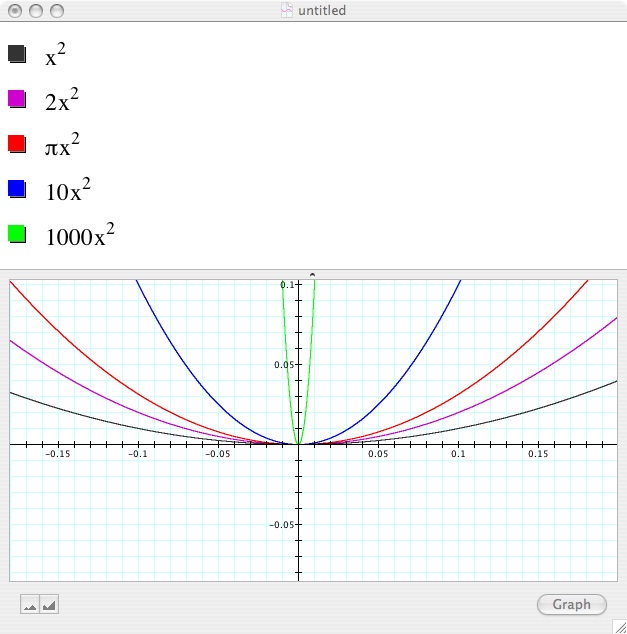
The window must be very small
to show these 5 functions clearly. The black function is the
original function y = ax². Notice that as the value of
a increases, the width of the parabola decreases. This pattern is
consistent with both rational and irrational numbers greater than
one.
Next, take these same equations
and make each value of "a"
negative.
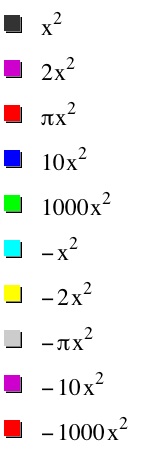
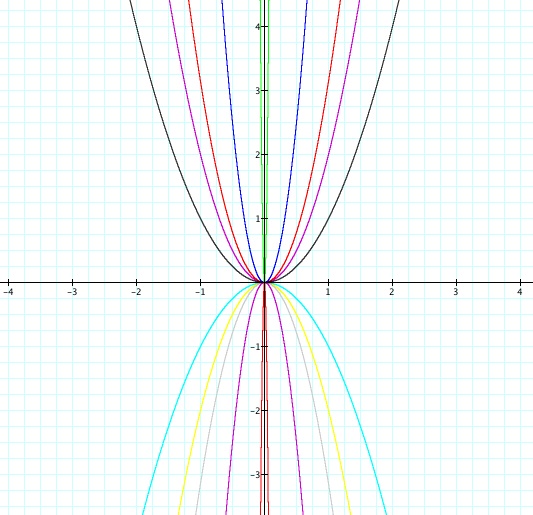
This time the window is slightly
larger. This enables us to get a
larger scale view of what is happening to these graphs. Notice
that in each case, when "a" becomes negative, the graph of the
function is reflected over the x axis. Remember that we're
still restricting our investigation to values of "a" whose absolute
value
is greater than 1.
We'll now explore values of "a"
greater than -1 and less than 1.
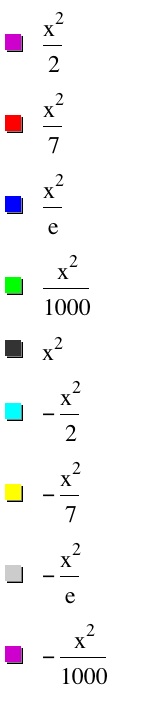
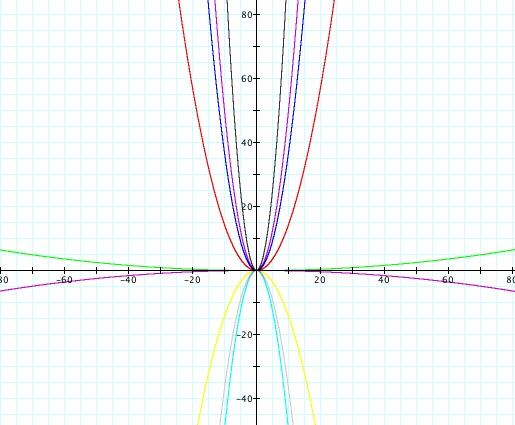
Notice first that these equations
are again reflected over the x axis
when "a" is negative. The black function is our original function
y = x². When 0
< a < 1, the function is wider
than the original function. As the absolute value of "a" becomes
smaller the function becomes wider.
We can summarize our findings
as follows:
Any equation of the form y = ax² will always be centered at the
origin.
When a > 0, y
= ax² opens up.
When a < 0, y
= ax² opens down.
When a = 0, y =
ax² is a horizontal line at y = 0.
When |a| > 1, y
= ax² is narrower than y = x². The larger |a|,
the more narrow y
= ax².
When |a| < 1, y
= ax² is wider than y = x². The smaller
|a|, the wider y
= ax².
In general, |a| and the width of y = ax² have a direct
negative relationship.
Now that we have
explored the function y = ax², try the following on
your own.
Tell in words what the graphs of the following equations will look like
compared to the graph of y = x².
a) y = (-2/3)x²
b) y =
(-3/2)x²
Which of these graphs will be wider, a or b?
c) y = 5x²
d) y = 2.5x²
Which of these graphs will be wider, c or d?
Return to my homepage