

First off, I constructed the picture of the orthic triangle and the triangle created by the intersection of the altitudes and circumcircle in GSP.
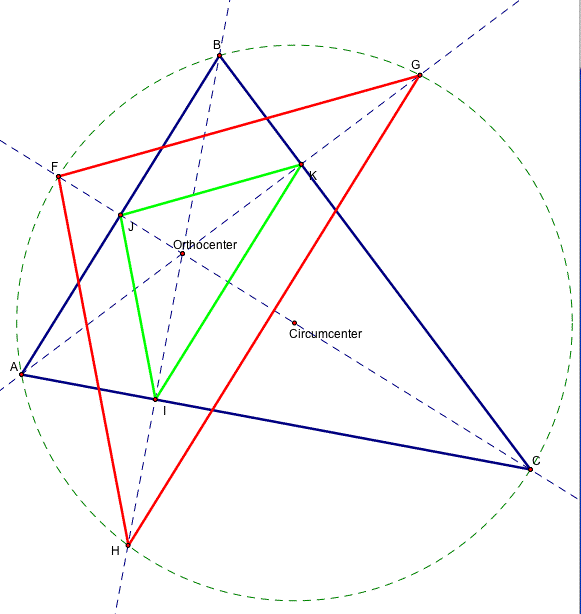
The blue triangle is the original triangle, the green triangle is the orthic triangle, and the red triangle is the triangle created by the intersection of the altitudes and the circumcircle. Through my explorations I realized that the line through F and the orthocenter is an angle bisector. This is true for the other lines through G and the orthocenter and H and the orthocenter. This means that the orthocenter for triangle ABC is the incenter for triangle FGH.
As is clear from the picture, the green and red triangles are similar. As I measured in sketchpad, I saw that the scale factor for the two triangles is 2. Click here to open a GSP file to explore this.
Now, I need to prove my claim that the triangles are similar and the scale factor is 2. From previous experiences, I know that the orthic triangle is on the nine point circle of triangle ABC. The nine point circle not only crosses through the feet of the altitudes but it crosses through the midpoints of the sides of triangle ABC.
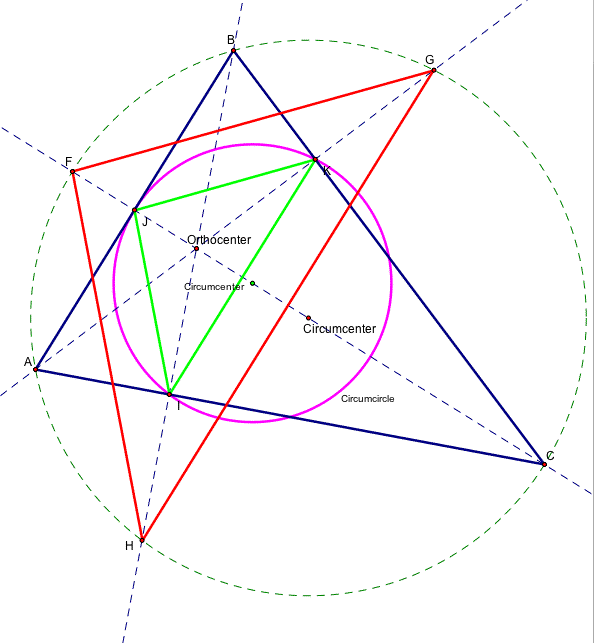
In the above picture, the purple circle is the nine point circle. This circle is similar to the circumcircle. Its scale factor is 2. The radius of the nine point circle is 1/2 the radius of the circumcircle.
Because the orthic triangle is inscribed in the nine point circle and the red triangle is inscribed in the circumcircle they have a ratio of 1 to 2. This is not only because of the relationship between the nine point circle and the circumcircle but also due to the fact that vertices of the triangles lie on the altitudes.
This experience was worthwhile in that it helped me really think through all that I thought I understood about the orthocenter, circumcircle, perpendicular bisectors, nine point circle, and altitudes. I would love for my students to have the same experience so that they have the opportunity to challenge what they know and understand.