To begin this problem, I used Graphing Calculator, a graphing program on the computer, and guess and checked. I honestly started working on this program two or three times. The guessing and checking aspect of it seemed hopeless to me. I would consider myself to be weak in graphing so this problem was a little intimidating. I also didn't feel confident in making adjustments based on my guessing because I am not confident in my graphing abilities.
Fortunately, one of my attempts at guessing proved fruitful. I graphed y = 2x + 1 and y = -2x. I had been guessing linear functions with 0 for a y-intercept and discovered that I wanted the slopes to be opposite. Then when I used this combination I got the following picture:
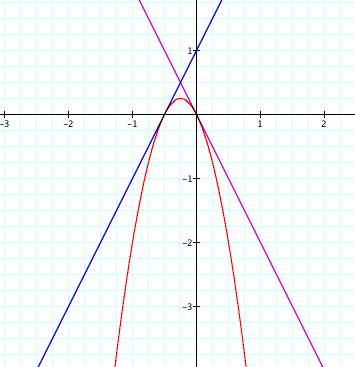
This discovery was really exciting! What I thought would be a fruitless adventure started to look worthwhile. So then I decided to see if the slope mattered. What if I changed the slopes of the lines? I wanted to keep them opposite but was the 2 what was lucky about my guess?
I used the "n" parameter in Graphing Calculator which is a slider. It allows you to vary the value of n and see its effect on the graph. Here is what it looked like:
So, it looks like the slope didn't matter. Next, I tried changing the y-intercept. I knew 0 wouldn't work from previous attempts, but what about 2?
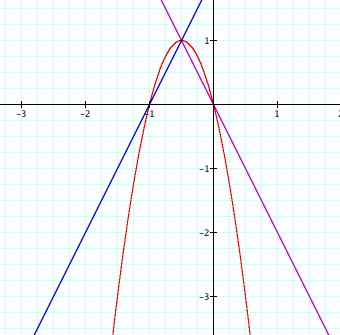
When I use 2 as the y-intercept I get 3 intersection points and the product is no longer a tangent to the two lines.
So, this got me thinking
algebraically. When will the vertex equal the intersection of
the two lines? Let the two linear functions be y = -nx + b and
y = -nx. When we solve for the intersection we get 
.
The product of these two linear functions are y = -nx(nx + b).
I solved for the vertex of this parabola and got 
.
Thus, the x-coordinates are always the same. So when are the y-coordinates
equal? When I solved this I got b = 0 or 2. This explains what
was happening when the y-intercept equaled 2. The vertex of the
parabola and the intersection of the two lines were equal. The
same thing will happen when the y-intercept is 0.
The next idea I considered was do I want the y value of the intersection point greater than the y value of the vertex?
To answer this question I graphed b = 3.
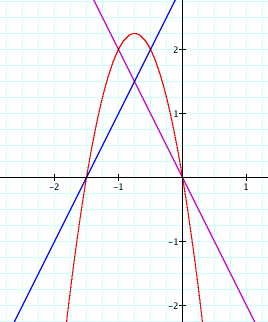
This shows the vertex greater
than the intersection point. This is a problem because I no longer
have a parabola tangent to the two lines. I definitely need the
vertex to be less than the intersection point. So, algebraically,
when does this happen? In other words, when does 
?
I solved this and found that 0 < b < 2.
This means a possible solution to the problem of finding two linear functions whose product is tangent to each line at exactly one point is when the equations are of the form y = nx + b and y = -nx where n is any thing except 0 and 0 < b < 2.
This made me wonder does it work if y = -nx + b and y = nx? I would say yes and predict that nothing in the picture would change. Let's see what happens...
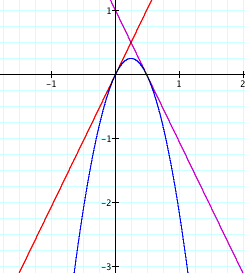
My prediction was correct! So I leave you with this question: Can you get the parabola to open up?