
Bouncing Barney

Bouncing Barney is a problem that takes place in a triangle. Barney chooses a starting point on the triangle and travels parallel to a side. Once Barney reaches a side of the triangle he must change direction. He cannot travel back to where he came from.
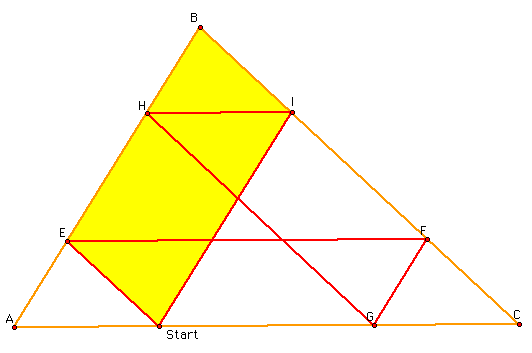
Here is a picture of Barney's path:
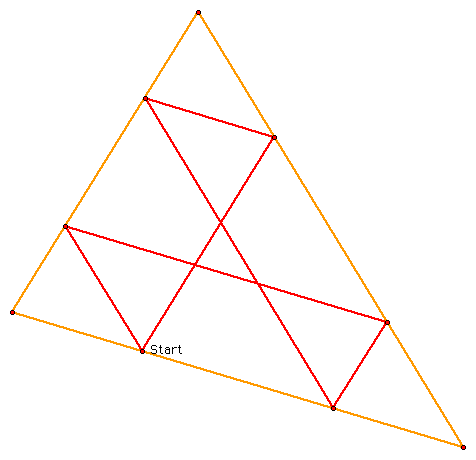
The red segments are Barney's paths. What may or may not be surprising is that Barney ends up where he begins. So the question is can we prove this?
Let's begin with Barney starting at a midpoint.
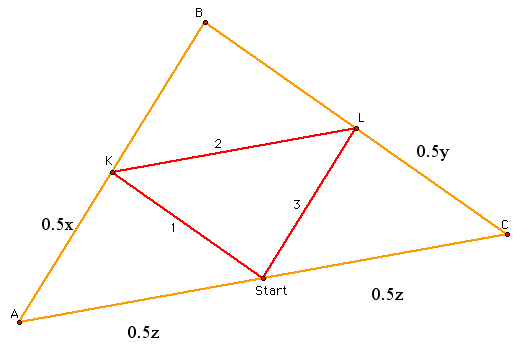

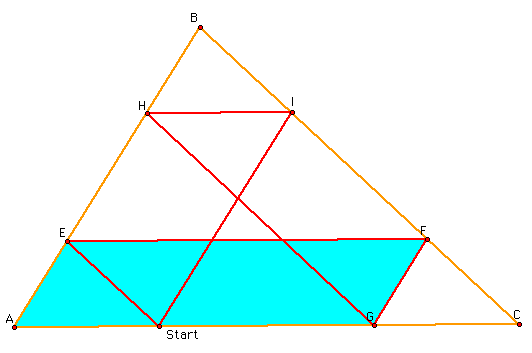
So is it also true if Barney starts somewhere else - besides the midpoint?

As I typed all this up, I wondered what would happen if you looked at angle measures instead. Here is a picture to show what I mean:
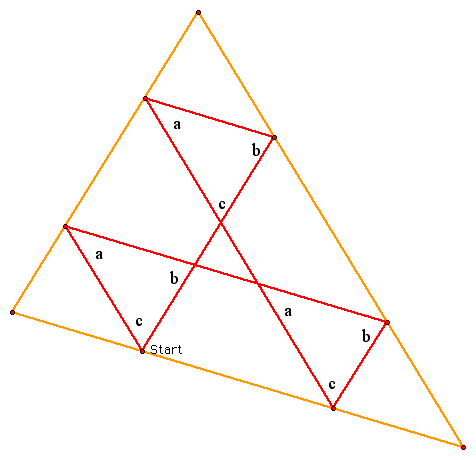
If we look at the places where Barney "bounces" off the walls, we see that the angles are a, b, c, a, b, and c. If we add them together we get 2a + 2b + 2c. If we look back at our picture we see that a + b + c = 180. This is true because the angles are the interior angles of a triangle. This means that 2a + 2b + 2c = 360. So is this a good argument for why Barney ends up back where he started? Because he walked in 360 degrees?
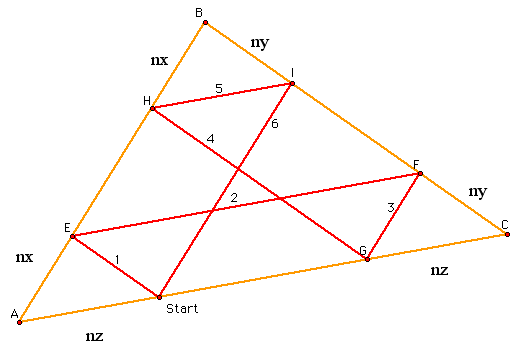
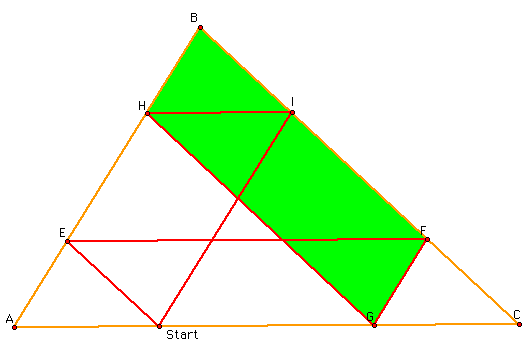
Finally, I was looking at the pictures I saw that Barney's path looked like the perimeter of the original triangle. Here is my proof for that:



The next situation to explore is what if we extend the walls of the triangle and start Barney outside of the triangle?
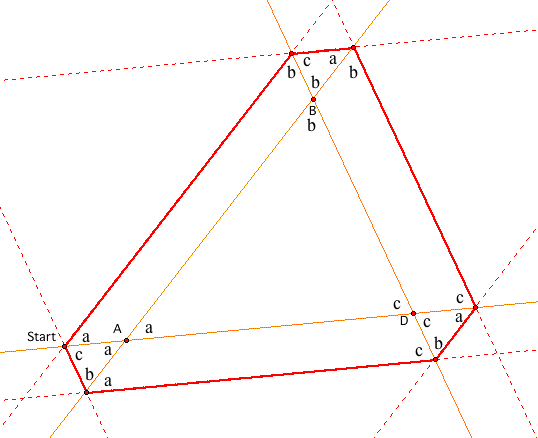
As you can see, I have carefully labeled the angles in the picture. Remember this picture is full of parallel lines. This is why the angle measures are repeated. If I look at Barney's path and start adding the angles I get a + b + c + a + b + c + a + b + c + a + b + c. From our original triangle ABD, we see that a + b + c = 180. Thus Barney's angles are 4 (a + b + c) = 4 (180) = 2 (360) = 720. Thus, Barney will end up at the Starting point because he has basically traveled in two circles.