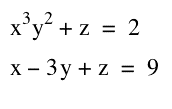Multiple Solutions

The problem we were given is to find all possible solutions to the system:
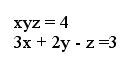
You will notice that this is a system of two equations and three unknowns. That makes this a little challenging!
To start, let's think about the signs of our variables. If we look at the first equation it appears that they all have to be positive or two of them can be negative. How does this impact the second equation? It doesn't seem to have much of an impact. Maybe we should graph them and see...
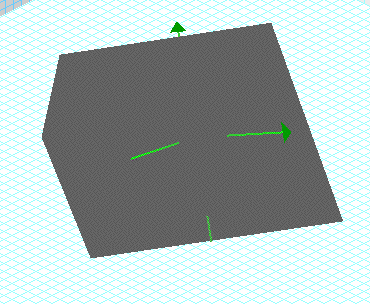
Here is the graph of xyz = 4:

The arrow pointing up is the positive y axis. The arrow to the right is the positive x axis. The z axis is positive as it moves towards us (the green line in the bottom left corner). From this graph we can see that we get four distinct pieces. The one in the center of the picture is all three positive. The bottom right graph is x positive and y and z negative. The bottom left graph is x and y negative and z positive. The graph in the back is y positive and z and x negative. So we were right about our values.
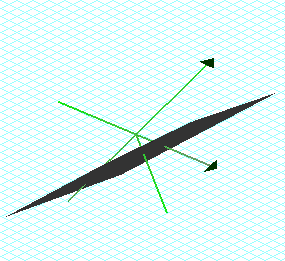
Now let's look at the second equation: 3x + 2y - z = 3:
This graph is a plane. Its not as interesting as the last one! From the graph we see that x ,y and z are positive and negative. If I look at the graph from a different perspective that is more clear:
Now our job is to find where these to graphs intersect. Let's graph them both together:

It looks like our solution will never be with x and z negative! However the other three sections of the red graph seem to be part of the solution. In order to get a better look at the solution, let's solve for z and substitute it in the second equation:
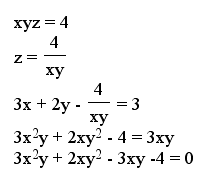
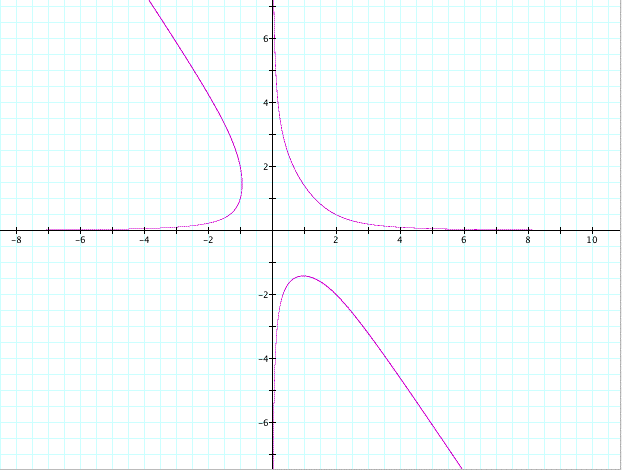
These graphs represent the solutions to the system. There are infinitely many solutions and the solutions need to lie on one of these three pieces of the graph. I spent some time trying to figure out the equations or something close to the equations for these pieces. They look like parts of hyperbolas but the guessing and checking seemed to be fruitless.
Here is another interesting system of equations: