
Locus of Vertices

The idea behind this investigation is to figure out what the locus of the vertices of the set of parabolas graphed from y = x^2 + bx +1. Then the challenge is to extend this to all parabolas.
I began by graphing a few parabolas on Graphing Calculator. Then I started to think algebraically. I wondered how to find the vertex of any parabola given in standard form. Here is my algebra to find the vertex:
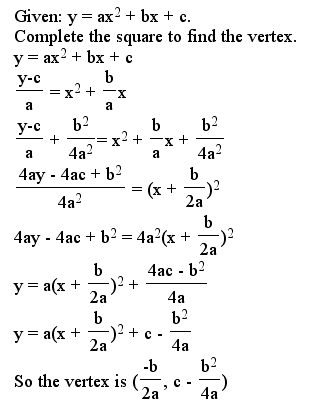
In the example, we are focusing on a = 1, b = b, and c = 1. So the vertex of these parabolas would be of the form
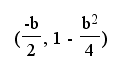
In order to get a picture of what these points look like for a variety of values of b, I decided to use parametric equations. I set the x = x-coordinate and the y = y-coordinate. Here is a picture of what the graph looks like:
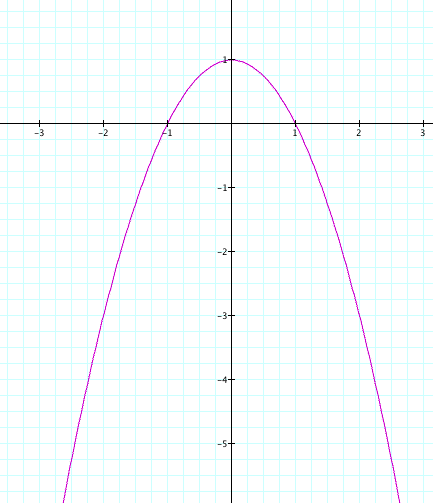
Are you surprised that its a parabola? To find the equation of this parabola, let's solve the x equation for t and plug it into the y equation.
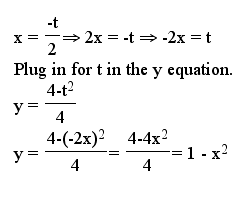
So, now that we've found the equation for the parabola that is the locus of the vertices of parabolas with the equation y = x^2 + bx +1, let's see if we can generalize this. We know that the vertices of parabolas with the equation y = ax^2 + bx + c is
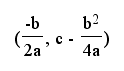
So we can graph this the same way that we did earlier. Unfortunately, I can only use one variable at a time to vary. So let's let a = n, b = t, and c = 2. Here is a picture of what we get:
I can also create a picture where c = n and a = 2 or any other number. Click here to open up a Graphing Calculator file to see what this looks like.
Next, lets see if we can algebraically find the equation for the locus of vertices. It seems like its always going to be a parabola. Let's see...
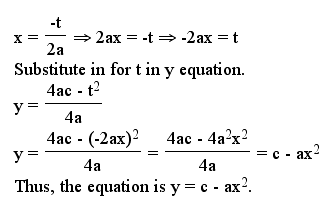
To generalize, we have shown that for any parabola of the form y = ax^2 + bx + c, the locus of its vertices forms a parabola with equation y = c - ax^2.