

The challenge in this assignment is to explore a polar equation. I decided to look at two:
I started with the cosine equation first. I varied a and kept b and k constant. Here are the graphs that I came up with:
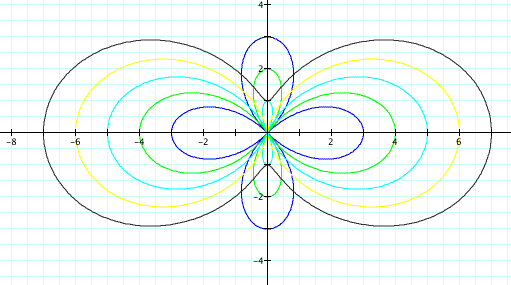
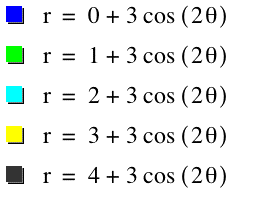
As you can see, when a = b the graph appears to have two leaves: the yellow picture. When a < b the graphs have 4 leaves but still all cross at the origin. When a > b the black graph does not cross at the origin and it has 2 leaves. The number of leaves is even in all our graphs and our k is 2. What would happen if we made k = 3?
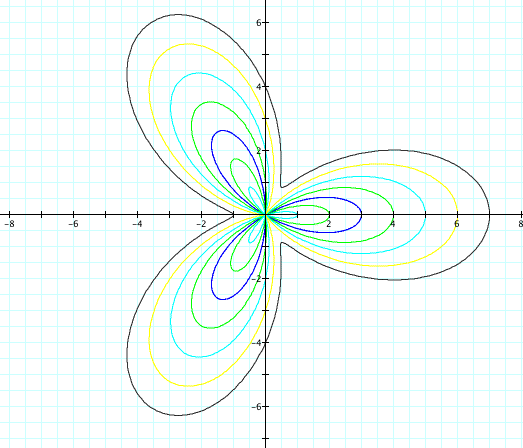
Now for all values of a we get three leaves. Interesting...a conjecture could be if k is even, the number of leaves is even and if k is odd, the number of leaves equals k. Let's explore this conjecture. Click here to open up a Graphing Calculator file that has a variety of equations already graphed with different k values. As you can see from the file, it appears our conjecture is correct. But that was with a = b. What if we vary a again?
If we look at when k = 4 and vary a, we see that when a > b, then the graphs do not touch the origin and have 4 leaves. When a < b, the graphs do cross at the origin and they have 8 leaves. Thus it seems like we can adjust our conjecture to when k is even and a > b, the graph has k leaves. When a < b, the graphs have 2k leaves. And finally, when a = b, the graph has k leaves.
Now, let's see when k = 5.
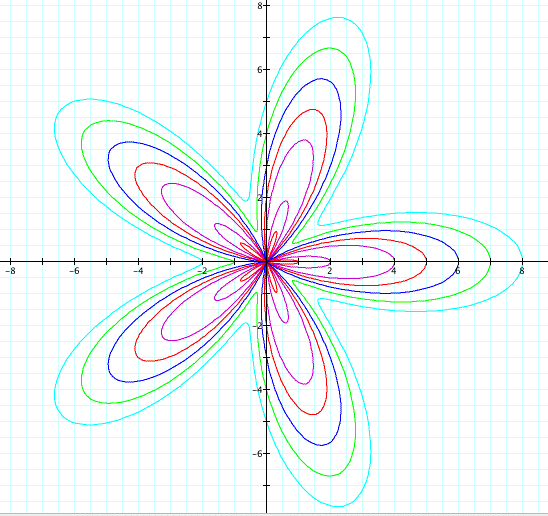
It looks like the same thing is happening here. The purple and red graphs have 10 leaves and that is when a < b. The dark blue, light green and light blue graphs have 5 leaves and that is when a > or = b. So it looks like the even/odd difference doesn't matter.
There are a few things left to address. Can we determine the x and y intercepts of the graph? Is it true that all odd numbers look tilted? We have been experimenting with b = 3 does that matter? What if a and b are negative? Will the graphs change if b = 2?
Let's deal with the last question first. I changed the equations used in the above graph so that b = 2.
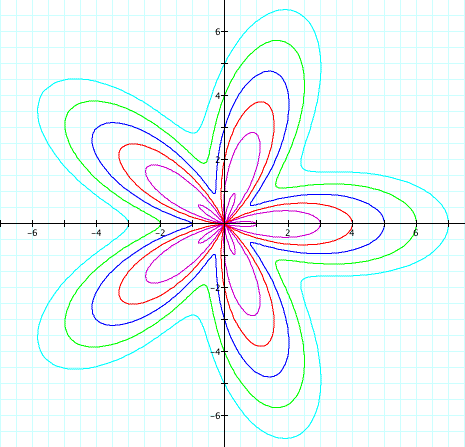
As you can see, b = 2 didn't really change much. It seems to effect the x-intercepts but our earlier conjectures appear to hold. So let's figure out the x - intercepts. Here is where even and odd k values seems to make sense to look at. Let's start with k = even numbers.
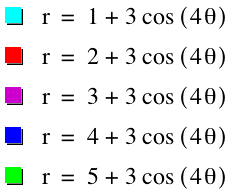
I'm going to organize myself with a table:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
It looks like a + b equals the intercepts for k = 4. The intercepts listed above are the x and y intercepts.
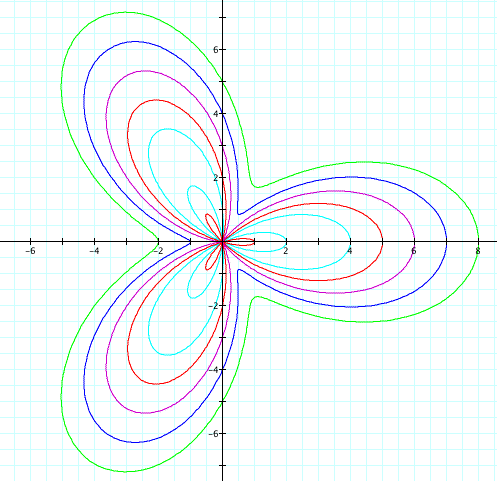
Now, let's look at k = 3 and see if we find a similar pattern.
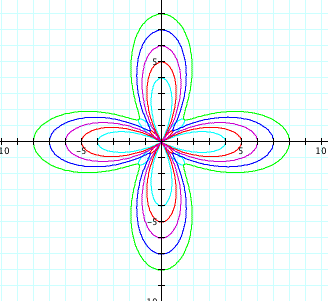
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In this case, it looks like the x-intercepts equal a + b and b - a. So now let's look at the y-intercepts.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The y-intercepts appear to equal +/-a. This isn't that surprising because our intuition would tell us that the value added on would effect the y values of the function. Although this is a little different because our equations are polar.
Conjectures:
When a > b, then the graph has k leaves. When a < b, the graph has 2k leaves and it crosses at the origin. And finally, when a = b, the graph has k leaves and crosses at the origin. If k is even, the x and y intercepts equal +/-(a + b). If k is odd, the x intercepts equal a + b and b - a. The y-intercepts equal +/-(a + b).
Now the challenge is to see if the same conjectures hold for
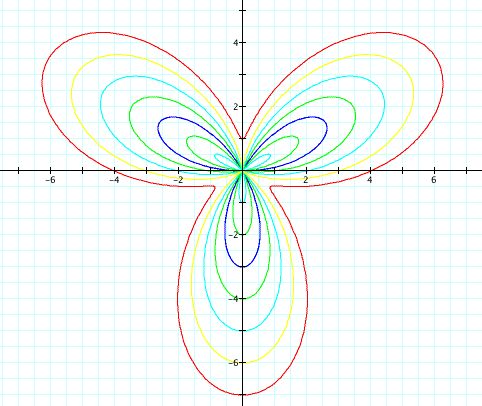
This is a graph of b = 3 and k = 2 with a varying. As you can see, these graphs have 3 leaves. Click here to open a Graphing Calculator file with k = 4. Use the file to play with the equation and see how our conjectures change for the sine graphs.