

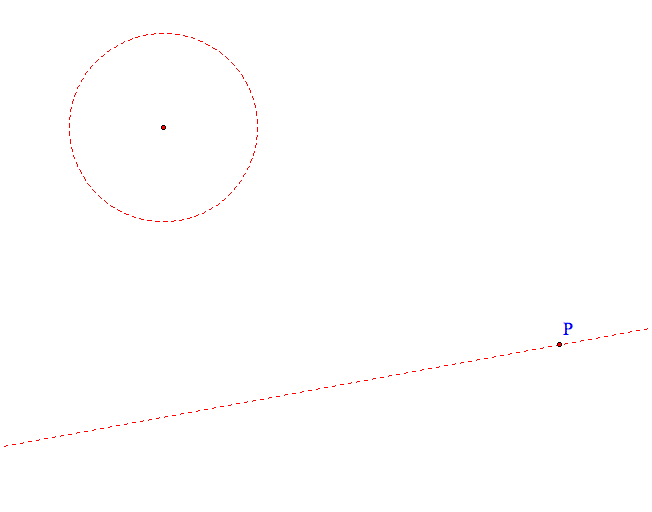
As I worked on this problem, I kept convincing myself that I could choose a point on the line and on the circle to construct the two tangent circles. Unfortunately this cannot be done if you are constructing! After many trials that yielded no results, I decided just to work with a point on the line. This problem challenges you to use a lot of information you know about circles, tangency, and perpendicular bisectors. I highly recommend it as a problem in a high school geometry course!
I decided to first focus on determining where the center of one of the tangent circles exists. I knew that it had to lie on the line perpendicular to the given line at point P. Remember the radius will have to be perpendicular to the given line. I knew that the center would also have to lie on the line connecting the center of the given circle through the point of tangency. But the problem is I don't know the point of tangency! So, what else do I know? I know that the center of the circle is equidistant from the two points of tangency! But I only have one!
So, what if I used the center of the given circle (since I know that!) and something connected to P? If I focus on the center of the given circle then the distance from that to the center of the tangent circle will equal the radius plus the radius of the given circle. Look at the following picture for clarification:
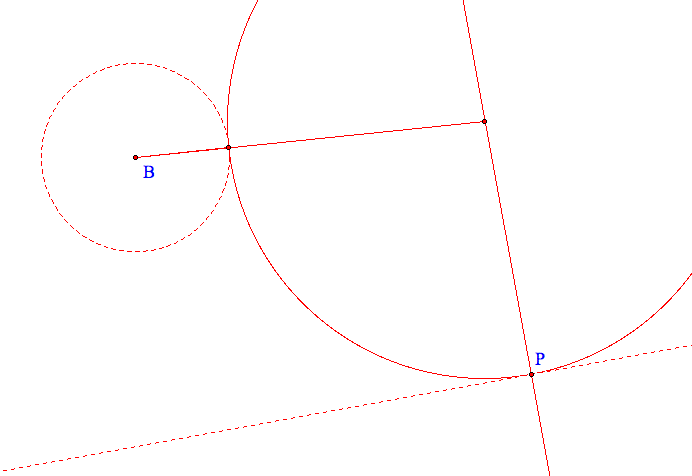
Now, remember that the tangent circle above is imaginary - we haven't found it yet! But I can recreate this imagined line segment on my perpendicular line through P. If I could mark the radius of the given circle beyond P on the perpendicular line then I would have know the endpoints of two segments that are equidistant from the center of our mysterious tangent circle.
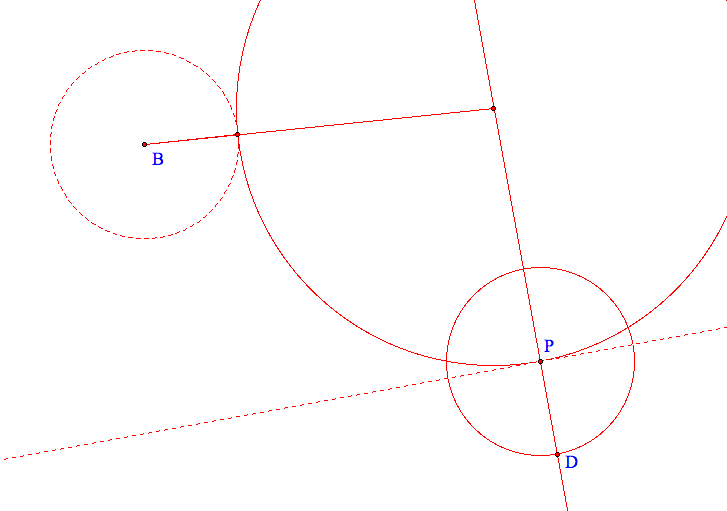
I can create the circle with center P and radius equal to the given radius without knowing my tangent circle. That is helpful because then I have two points that are equidistant from the center I'm looking for. I can find the center by constructing the perpendicular bisector of the segment BD. Where this perpendicular bisector intersects my perpendicular through P is the center of my tangent circle. Its radius is the distance from the center to P.
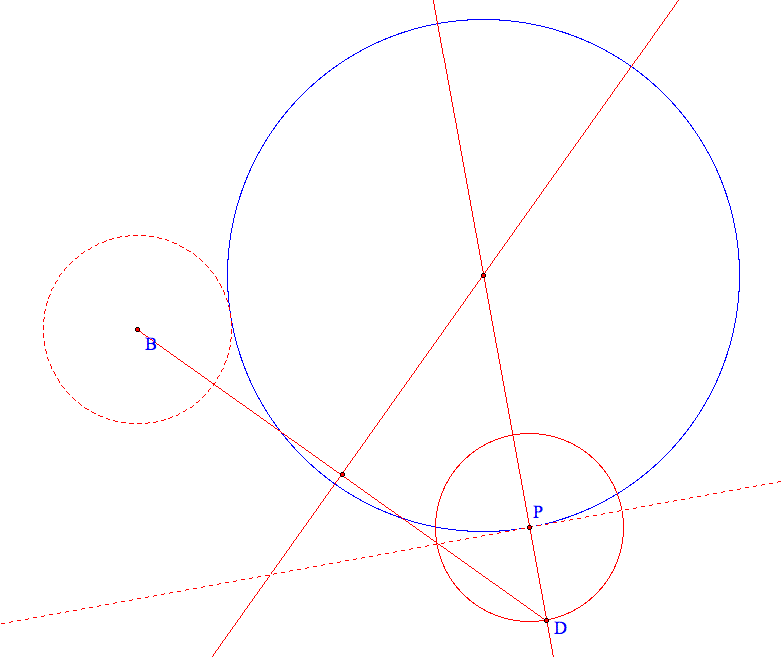
The blue circle is the tangent circle. We did it!
Now, how to find another tangent circle? Let's look at the the original problem again and brainstorm.

Ok, we know that the center of our tangent circle needs to be on the line perpendicular to the given line through P. If we want it different from our first tangent circle than we need to imagine the tangent circle hitting the "other side" of the circle. Here is a picture of the situation that I did not construct but just fiddled with on Sketchpad:
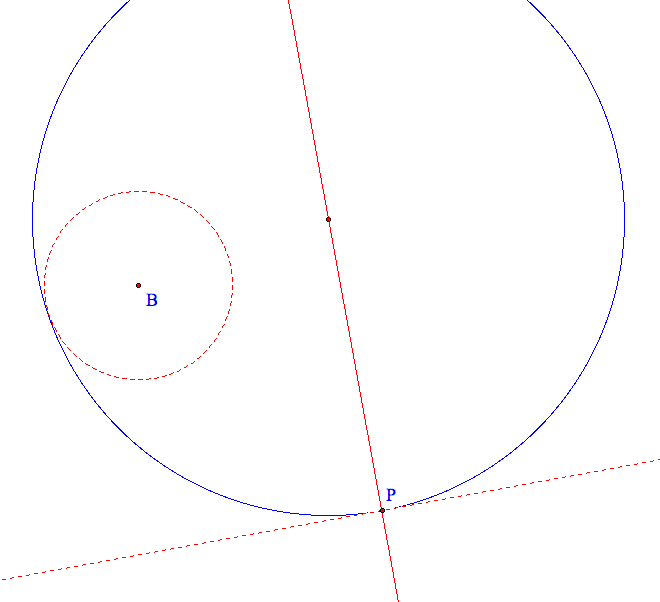
If I look at the segment from B to the center than we know that it will equal the radius of the blue circle minus the radius of the given circle. We can do that by constructing our circle about P again! Then do the perpendicular bisector "trick" again and we've got it!
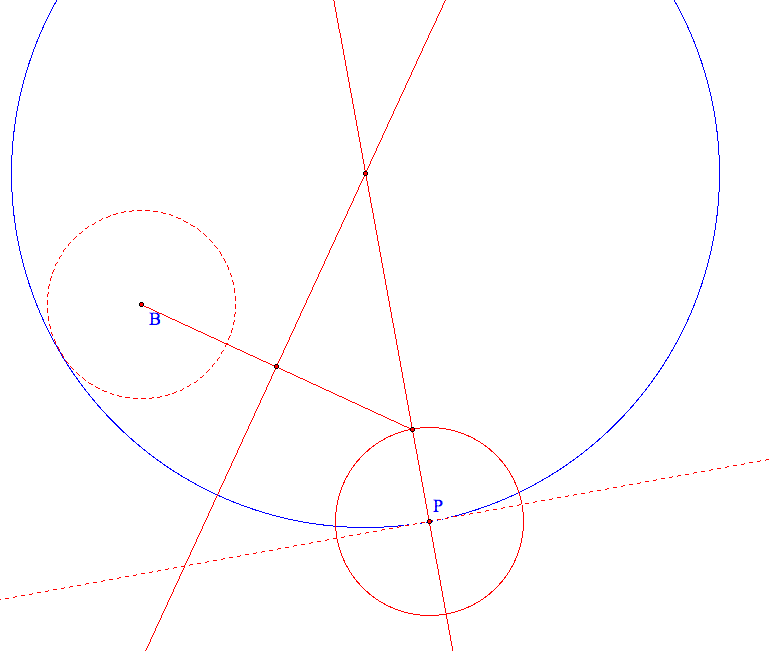
We did it! Now, after all that let's look at the centers of the two tangent circles as P moves. Click here to open a sketchpad file that has this animation in set up for you.
So, what did you notice? They look like parabolas, right? Let's think... does that make sense? YES, because isn't that the basic definition of a parabola: the set of points equidistant from a line (directrix) and a point not on the line (focus).