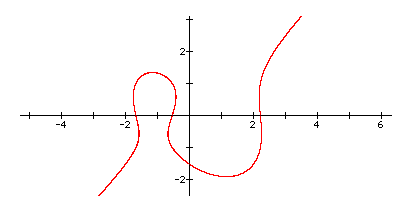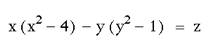EMAT 6680 Assignment 1

 

Victor L. Brunaud-Vega

For each of the following items, I used the Graphing Calculator 3.5 program, to explore, understand, and extend.


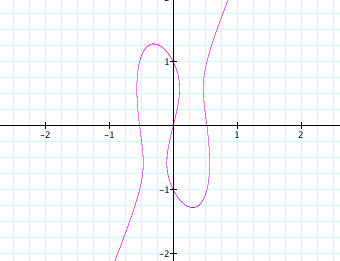
1. Examine:

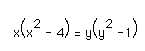
What happens if the 4 is replaced by other numbers (not necessarily integers)? Try 5, 3, 2, 1, 1.1, 0.9, -3.  Any unusual event?  Interpret.

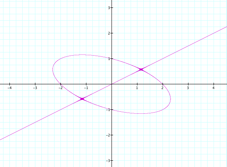
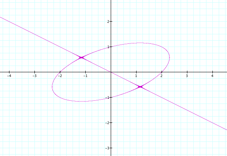
Let us rename the constant 4 as ÒnÓ. Then, we have:

x (x2 - n) = y (y2 - 1)

Using the software ÒGraphing CalculatorÓ I made this animation, where we can see that, when n=1, it appears an oval crossed by its center for a straight line.

 

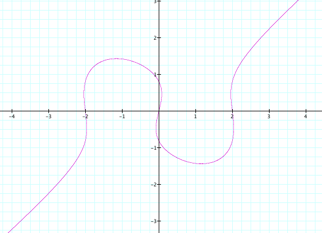
What equation would give the following graph?:

 

I started using the original equation

x (x2 - 4) = y (y2 - 1)

because it looks more symmetric.  As a consequence of the previous exploration I knew that ÒnÓ wouldnÕt help in this case, so I had to break the symmetry in a different way.  Adding a constant to the first term, I found that

x (x2 - 4) + (-2.1) = y (y2 - 1)

gives me something similar to the original picture, as you can see.

My question now is: May I find the same graphic adding a constant in the second term of our original equation?  Of course, it is only a thing of adding 2.1 to the second term and we have the same graphic.

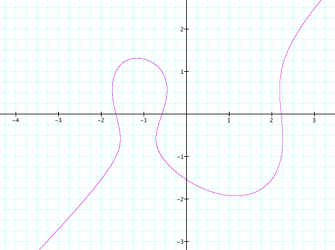
Actually, there is a group of values that produce similar graphics.  If you are adding a constant to the first term of the equation, then you can produce a similar graphic using one of the values between -1.6 and -2.3, as you can see in this animation; the same effect is produced if you add a constant with value between 1.6 and 2.3 to the second term of the equation, as you can see in this animation..

 

 

What happens if a constant is added to one side of the equation?

 

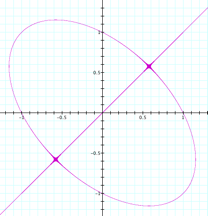
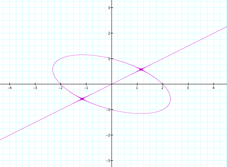
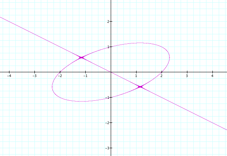
First, I tried with a constant on the right side as

And the graphic shows a straight line passing by the origin of the system (0,0) and projecting itself through the first and third quadrants, crossing an oval, centered in the origin, when the constant has a value of 8.

Now, what happens if I make  n = -8 ?   Then we have a graphic showing a straight line passing by the origin of the system (0,0) and projecting itself through the second and fourth quadrants, crossing an oval centered in the origin.

Here is an animation to explore the situation.

n = 8

n = -8

 

 

Let us try a different variation of the given formula, using a constant:

In this case, it is produced a straight line crossing the origin of the system (0,0) and having a nice behavior, because whatever is the locus of the line in the first and fourth quadrants, exactly the opposite is the behavior of the line in the second and third quadrants.

Here is an animation to enjoy this situation.

 

 

Now is time to try these variations in the first term of the given equation.  Then, we begin multiplying the factor x by the constant n, so:   

Again we have the straight line crossing the origin and the oval centered in the origin, although this time the value of n = -0.13 or n = 0.13

Here is an animation to watch the situation.

 

n = 0.13

n = -0.13

 

Then we try the other variation:

The result, as at the beginning a straight line crossing the origin of the system (0,0) and having a nice behavior, because whatever is the locus of the line in the first and fourth quadrants, exactly the opposite is the behavior of the line in the second and third quadrants.

Here is an animation to explore.

 

 

Try graphing

 

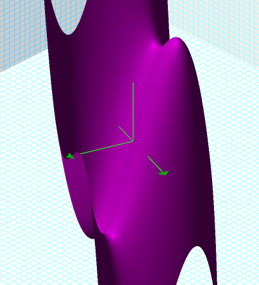
Funny, hah?  See the graph here.

 

Well obviously z represents a third dimension.  Now, what happen if I try a variation in the first term of this equation?

Here are some animations to explore those situations:

 

 

 

   Return to my Class Page


          Return to EMAT 6680 Home Page.