|
|
|
|
|||
|
|
Assignment #11 Polar Equations |
|
|||
|
|
By Victor L. Brunaud-Vega |
|
|||
|
|
|
|
|||
|
|
1. Investigate
Note: * When a and b are equal,
and k is an integer, this
is one textbook version of the
"n-leaf rose." * Compare with
For various k.
What if . . . cos( ) is replaced with sin( )? |
|
|||
|
|
|
|
|||
|
|
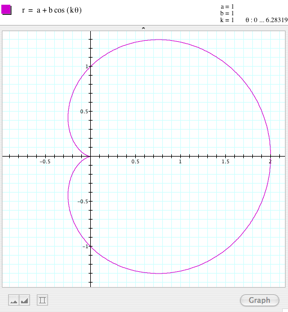
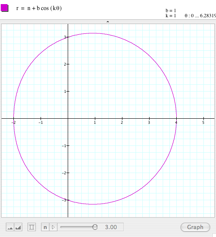
Let us start graphing the first
equation r= a + b * cos
(kŻ) |
|
|||
|
|
|
It looks like a peach! But that is not relevant. But I have no clues, just questions:
what is controlled by the parameter a? And b? What happens if we give several values to k? |
|||
|
|
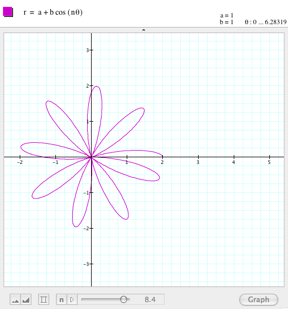
What happens if we give different
values to k? The picture a right
shows the effect, the flower mentioned in class. What is controlled by the parameter k? |
|
|||
|
|
|
|
|||
|
|
|
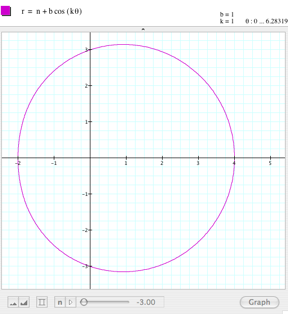
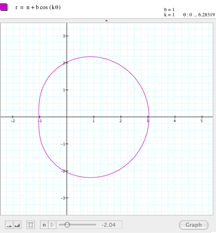
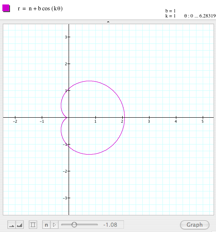
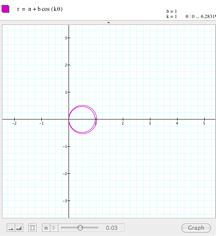
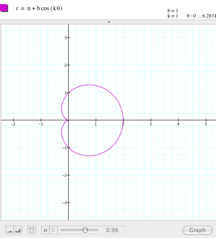
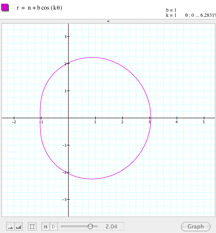
This is frustrating. Let us try keeping b=1 and k=1, and giving different values to a. I tried a range between
-3 and 3, and the result is amazing.
As you can see in the set of pictures below, if a=3 or a=-3, the graph shows a circumference centered in (1,0). Here
is a movie showing the entire sequence. It looks like a controls the radius of the circumference and probably b controls the center of the
circumference. |
|||
|
|
|
|
|||
|
|
|
||||
|
|
|
|
|||
|
|
|
||||
|
|
|
|
|||
|
|
|
||||
|
|
|
|
|||
|
|
Let us try now keeping a=1 and k=1, and giving different values to b. |
|
|||
|
|
Here
is a movie showing the whole sequence. |
|
|||
|
|
|
|
|||
|
|
There is a displacement of the center
through the x axis as the value of a changes. |
|
|||
|
|
|
|
|||
|
|
|
||||
|
|
|
|
|||