Assignment # 4 Centers of a Triangle by Victor L. Brunaud-Vega
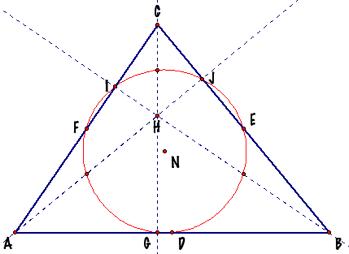
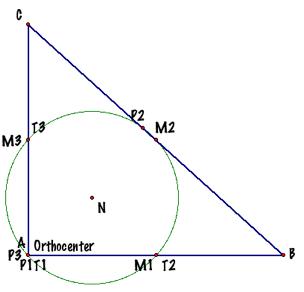
The Nine-Point Circle for any triangle passes through: · The three mid-points of the sides; · The three feet of the altitudes; and · The three midpoints of the segments from the respective vertices to the Orthocenter.
Three points in the same plane but not in the same line are common because that is the geometrical way to define a circumference. Four points in the same circumference are more rare. But nine points! Come on! Does it work for any triangle?
Well, this animation says yes. If you can’t see it, maybe you should try here.
What is the center of this circumference?
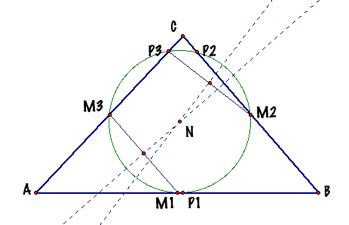
To construct the middle points was easy, as well finding the feet of the altitudes, but how can we find the center of the circumference? We know the perpendicular bisectors of chords always go through the center of the circle. So we can find the center by connecting two pairs of points with line segments and intersecting the perpendicular bisectors of the chords, as shown in the picture.
Maybe is interesting to revise some situations in which some points coincide collapsing and becoming not in nine but in eight or less points.
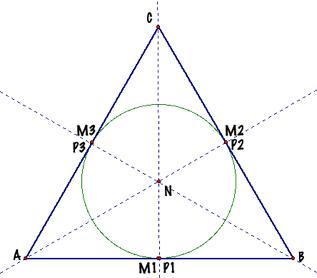
	For example, if the triangle is equilateral, the middle points of the sides coincide with the feet of the altitudes of the triangle, so the circumference shares only three points with the triangle.
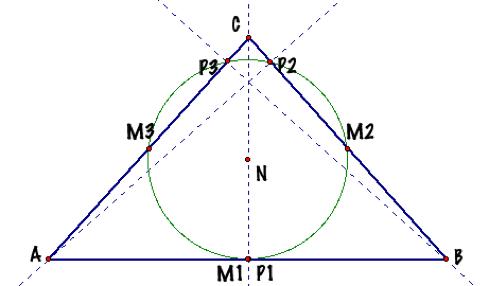
	And if the triangle is isosceles, the midpoint and the foot of the altitude of the base coincide, so the circumference shares only eight points with the triangle as is shown in the picture below.
	In a right triangle ABC, the feet of the heights based on the legs coincide with the vertex where each leg meets the hypotenuse. In this case, we have only five common points between the triangle and the circle. So, the center of the circle is in the midpoint between the midpoint of the hypotenuse and the vertex of the other two sides of the triangle, as you can see here.
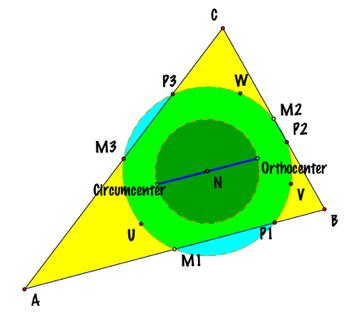
THE CENTER OF THE 9-POINTS CIRCLE IS THE MID-POINT BETWEEN THE ORTHOCENTER AND THE CIRCUMCENTER.
Another interesting characteristic of this Nine-Points Circle is that its center (N) is the middle point between the Orthocenter and the circumcenter, as we can see in the picture and in this animation.

	Return to my Class Page
	Return to EMAT 6680 Home Page.