border=0 EMAT 6680 Assignment 6


EMAT 6680 Assignment 6

Explorations with Geometer's Sketchpad

By Victor L. Brunaud-Vega

Construct a triangle and its medians. Construct a second triangle with the three sides having the lengths of the three medians from your first triangle. Find some relationship between the two triangles. (E.g., are they congruent? similar? have same area? same perimeter? ratio of areas? ratio or perimeters?) Prove whatever you find.

 

 

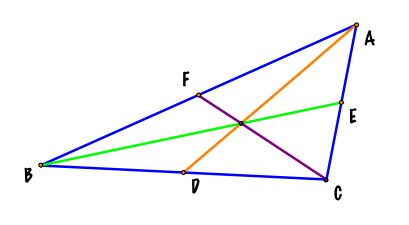
I started constructing a triangle ABC and its medians AD, BE, and CF.

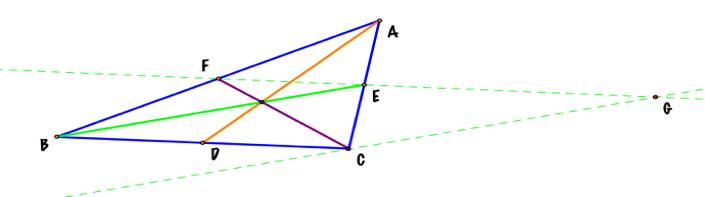
Then I traced a line at point C, parallel to the median BE, and another line at E, parallel to the side BC.  These two lines have one point of intersection G.  The segment CG has the same length and orientation than the median BE.

 

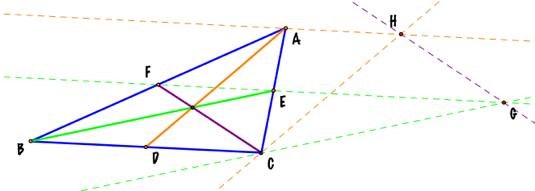
Then I traced a line at C, parallel to the median AD, and another line at A, parallel to the side BC.  These two lines have one point of intersection H.  The segment CH has the same length and orientation than the median AD.

 

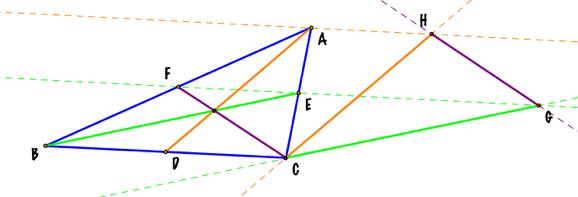
I continued tracing a line at point G, parallel to the median CF, which contains point H.  The segment GH has the same length and orientation than the median CF.

 

The sides of the triangle CGH have respectively the same lengths than the medians AD, BE, and CF of the triangle ABC.

 

This animation shows how unique is triangle CGH.  If triangle ABC changes, triangle CGH changes also.

 

 

This animation shows that there is a constant relationship between the areas of both triangles: the area of the triangle of medians is three-fourths of the area of the given triangle.

 

 

This animation shows that the ratio of the perimeter of the triangle to the perimeter of the given triangle never is less than .75 or more than 1.0

 

 

 

 

 

 

 

  Return to my Class Page


          Return to EMAT 6680 Home Page.

border=0