|
|
by Victor L.
Brunaud-Vega |
||||
|
|
|
|
|||
|
|
1.
Construct any triangle ABC. |
||||
|
|
|
||||
|
|
2.
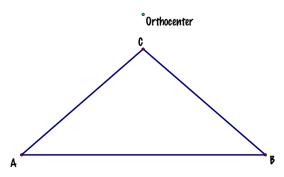
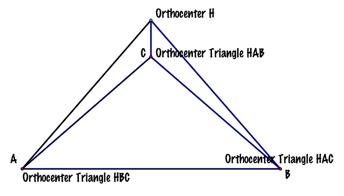
Construct the Orthocenter H of the
triangle ABC. LetÕs remember:
the orthocenter of a triangle is the common
intersection of the three lines containing the altitudes. An altitude is a
perpendicular segment from a vertex to the line of the opposite side. (Note:
the foot of the perpendicular may be on the extension of the side of the triangle.)
It should be clear that H does not have to be on the segments that are the
altitudes. Rather, H lies on the lines extended along the altitudes. |
||||
|
|
|
||||
|
|
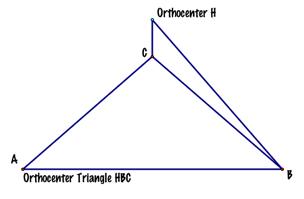
3.
Construct the Orthocenter of
triangle HBC. |
||||
|
|
|
||||
|
|
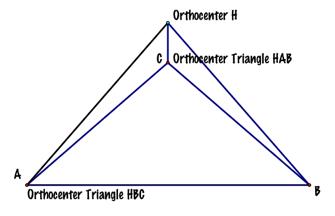
4.
Construct the Orthocenter of
triangle HAB. |
||||
|
|
|
||||
|
|
5.
Construct the Orthocenter of
triangle HAC. |
||||
|
|
|
||||
|
|
6.
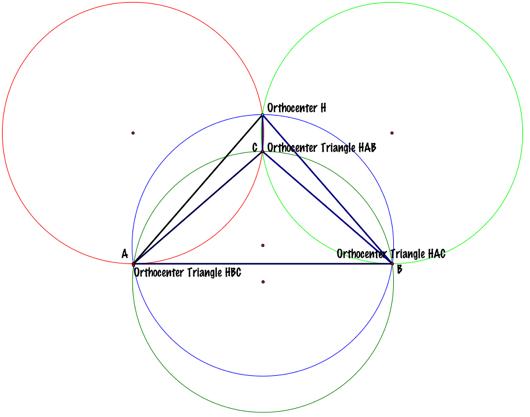
Construct the Circumcircles of
triangles ABC, HBC, HAB and HAC. |
||||
|
|
|
||||
|
|
|
|
|||
|
|
7. Conjectures? Proofs? |
|
|||
|
|
|
Conjecture 1: If triangle ABC is
rectangle, then: á Orthocenter
H coincides with vertex B (where the catets of triangle ABC meet). á Orthocenter
H coincides with the Orthocenter of triangle HAC. á The
circumcircles of triangles ABC and HAC coincide. á The
circumcenters of triangles ABC and HAC coincide with the midpoint of the
hipotenuse |
|||
|
|
|
|
|||
|
|
Conjecture 2: all four circumcircles are
congruent. Here
is an animation of triangle ABC, showing how the radii of circles c1, c2, c3,
and c4 is always the same, even if it is not constant. |
||||
|
|
|
|
|||
|
|
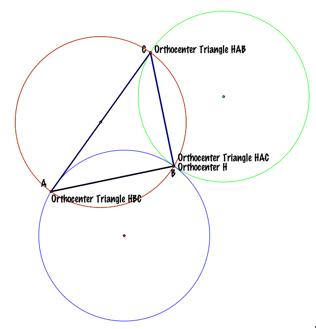
Conjecture 3: The orthocenters of
the three triangles formed by creating the orthocenter of the original
triangle, lie on the vertices of the original triangle. As you can see in the picture, the
orthocenter of triangle HAC is point B; the orthocenter of triangle HAB is
point C; and the orthocenter of triangle HBC is point A. This is valid for any triangle ABC,
as you can explore here. |
|
|||
|
|
|
|
|||
|
|
Conjecture 4: Given three congruent circles
with one common point, we can find a triangle ABC, its orthocenter H, and the
triangles HAC, HAB, and HBC, and its orthocenters. |
|
|||
|
|
|
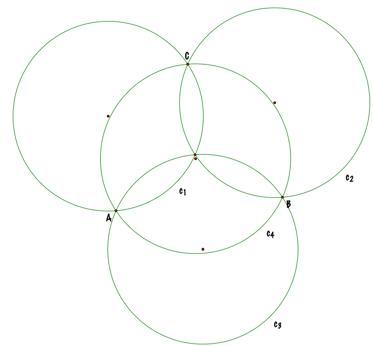
Constructing a fourth congruent circle (c4),
with a common point A with c3 and c1, and a common point
B with c3 and c2 , and a common point C with c1
and c2 , we have defined the vertices of our main triangle. Now, letÕs go for the orthocenter H, which is
the intersection among c1, c2, and c3. From this point H, orthocenter of the triangle
ABC, we can construct the triangles HAB, HAC, and HBC. |
|||
|
|
The centers of our original circles have became
the circumcircles of the mentioned triangles: |
||||
|
|
|
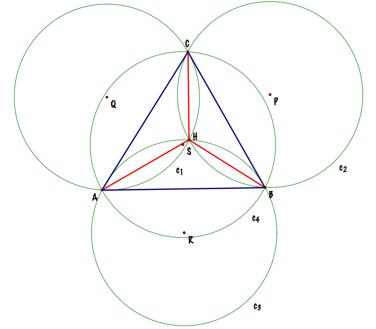
á The
circumcircle of triangle ABC is c4. á The
circumcircle of triangle HAC is c1. á The
circumcircle of triangle HAB is c3. á The
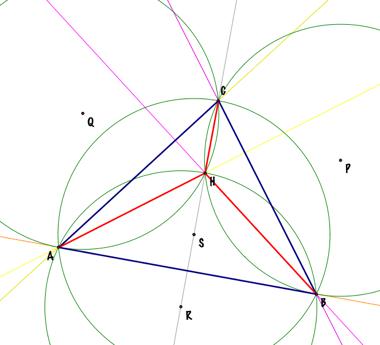
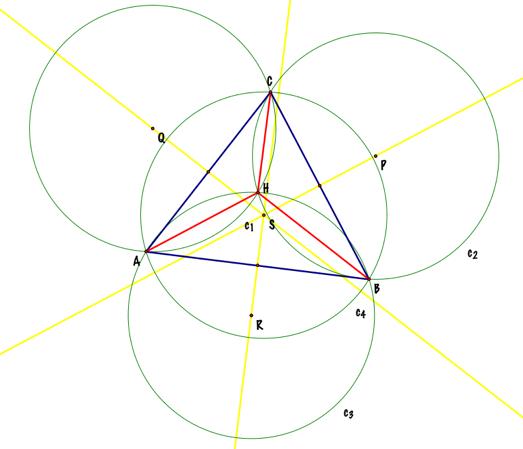
circumcircle of triangle HBC is c2. The centers of the circles c2, c1, and c3 (P, Q,
and R, respectively) are related to the perpendiculars to the sides of the
original triangle ABC. Here
is an animation to see these relationships. |
|||
|
|
As you can see in the picture below: á P
is part of the perpendicular to BC at its middle point; á Q
is part of the perpendicular to AC at its middle point; á R
is part of the perpendicular to AB at its middle point; á and
S is the intersection of the perpendiculars to the sides of triangle ABC at
its middle points. |
||||
|
|
|
||||
|
|
As I said before, the orthocenters of the
triangles HBC, HAC, and HAB are at points A, B, and C, respectively. |
||||
|
|
|
|
|||
|
|
Conjecture 5: When triangle ABC is acute
or rectangle, the sum of the areas of triangles CBP, ARB, and ACQ (formed by
the sides of ABC and the respective centers of the circumcircles of triangles
HAC, HBC, and HAB), is equal to the area of triangle ABC. Here
is an animation showing this relationship. |
||||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
||||
|
|
|
||||
|
|
|
||||