Assignment #9

Podal Triangles Explorations

by

Victor L. Brunaud-Vega

Constructing the podal triangle of ΔABC

Podal triangle when point P belongs to one of the sides of ΔABC

Podal triangle when point P belongs to ΔABC’s circumcircle

Podal triangle when point P belongs to the ΔABC’s incircle

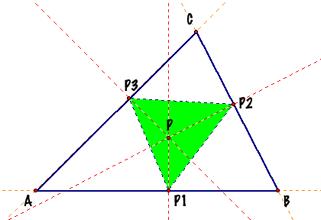
Constructing the podal triangle of ΔABC

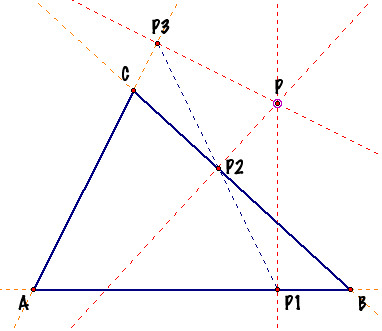
		In any triangle ABC, as in these picture, given some point P (which can be interior or exterior to the triangle), if we draw the three perpendicular lines from that point P to the three sides of the triangle (or to the projections of the sides, if it is the case), determining the points P1, P2 and P3.
Tracing segments among these points we have a new triangle, the PODAL triangle of ΔABC
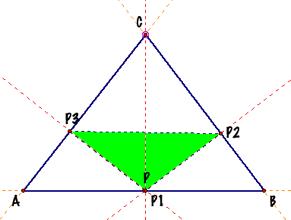
Podal triangle when point P belongs to one of the sides of ΔABC
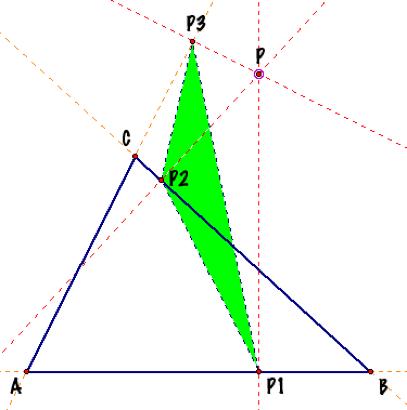
	When the point P belongs to the side AB of the triangle ABC, like in the picture of the left, both point P and point P1 are coincident. If the point P belongs to the side BC of the triangle ABC, both point P and point P2 are coincident. And if the point P belongs to the side CA of the triangle ABC, then both point P and point P3 are coincident. But the interesting effect of these situations is the relation between the angles. You can see relationships among some measurement of angles here.
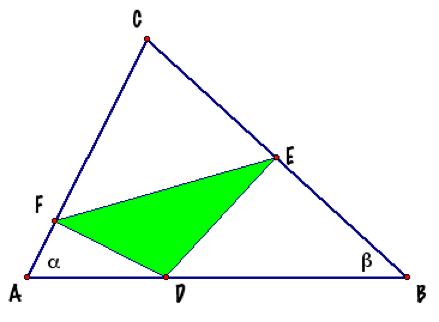
Another proof of this relationship is developed now.
Podal triangle when point P belongs to ΔABC’s circumcircle
This is beautiful. If the point P belongs to the circumcircle of the triangle ABC, the points P1, P2 and P3 become part of the same line and the podal triangle disappears. You can see an animation of this case here. As the point P moves following the circumcircle of the triangle ABC counter-clockwise, the segment to which belongs P1, P2 and P3 spins clockwise, and vice versa.
				If we trace the segment to which the points P1, P2 and P3 belong during the movement of point P on the circumcircle of the triangle ABC, we will get a rare shape, called tricuspid deltoid, relative to the deltoid muscle in the human shoulder.
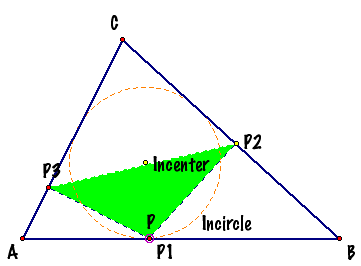
Podal triangle when point P belongs to the ΔABC’s incircle
I was exploring possibilities moving the point P along the incircle of the triangle ABC, but I could not find much new stuff. You can play an animation here. Even thought, the point P stays into the interior region of the triangle ABC and whenever the point P reaches one of the sides, it coincides with the correspondent point P1, P2 or P3.
Return to my EMAT6680 Class Page
Return to EMAT 6680 Page