Final Assignment – Part B

“Multiple Solutions”

By

Victor L. Brunaud-Vega

1. Find as many solutions as possible for A, B, and C that satisfy both equations: ABC = 4 3A + 2B - C = 3
What observations can you make about your results? Again, we discussed some approaches to this one in class. Your task is to prepare a write-up that explores this task. (Not required, but you might want to consider how to explore this one with a spreadsheet as well as with graphing tools.).
Okay, let's start looking at these surfaces in 3D, using the software Graphing Calculator and replacing x=A, y=B, and z=C. I will try the two equations separately to find their characteristics and try to analyze them.
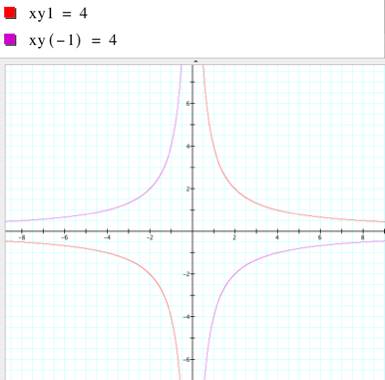
As we can see in the picture at right, the first equation, xyz=4, is a hyperboloid with the following characteristics: It doesn’t intersect any of the three axes x=0, y=0, z=0, in any point. For z > 0, the product xy must be positive, therefore the curve will exist in the first and third quadrant only for z < 0, the product xy must be negative, so the curve will exist in the sixth and fourth octants.
						If I project in plane the intersection between the hyperboloid and z=1 (red line, quadrants I and III) and z=-1 (blue line, quadrants II and IV), I get the picture at left.
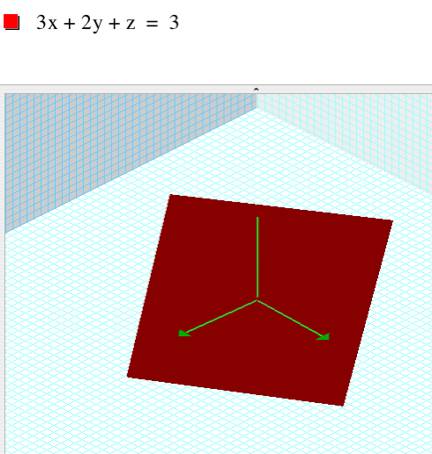
Now I will try the second equation using “Graphing Calculator” and replacing A, B and C by x, y, and z, respectively.
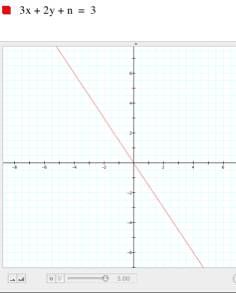
As you can see at right, the result of graphing the equation 3A + 2B + C = 3 is a plane. This plane will intersect the z axis (x = 0, y = 0) for z = 3. Keeping z=0, the graph in the plane shows the straight line you can see below
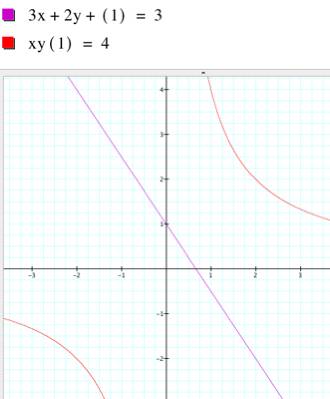
If I graph both equations now, maybe I will find a solution or more probably a set of solutions. Below there are some pictures of graphs using both equations.
Here is a file where you can explore this situation.
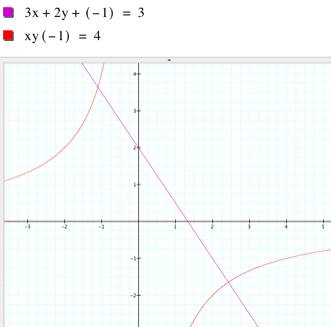
As we could see, there are many solutions. If z = - 1 there are two intersecting points, each in quadrants second (VI) and fourth (VIII), as you can see in the picture at right.
					If z = 1, there is no intersection between both surfaces. There is no solution for z=1.
Conclusions: § x and y can't both be negative. Observing the graphs, they never intersect on quadrant III. § x and y can't be negative if z is positive.
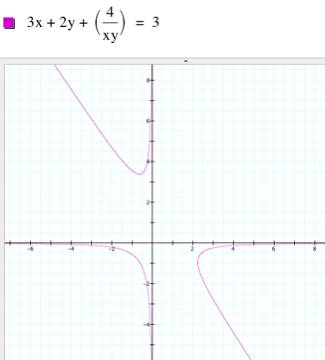
Let’s try something different: If ABC=4, then C=4/AB. Therefore, I can replace C in the second equation, obtaining: 3A + 2B + 4/AB = 3.
Now we can graph it, getting something similar to the picture at right. This is not helping to clarify the situation. Let us try a different approach.
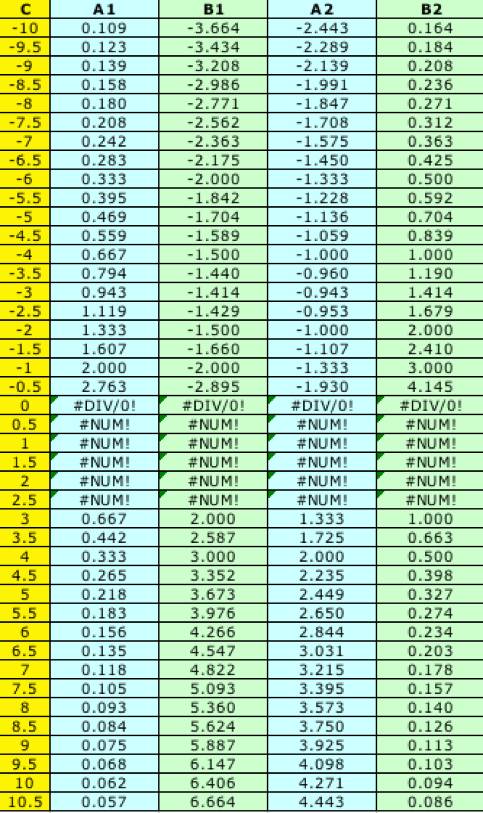
We can use Excel to explore a set of results, but these equations will not be useful. I need a new equation. Let us try saying that: If C= -2, then replacing C in the first equation, AB= -2. Therefore, A= -2/B. Replacing A in the second equation, we have: 3(-2/B) + 2B – (-2) =3. After simplification, 2B^2 – B -6 = 0 That gives us two values for B: 3 and -2, with x = 4/-6 and x=1, respectively. Can we repeat this procedure for any value of C?
							Not really, as we can see in this spreadsheet. When the value of C goes between 0 and 2.5, there are no solutions.

Return to my Final Page

---