Final Assignment – Part 2.C

Stamp Data

by

Victor L. Brunaud-Vega

Consider the Stamp Problem in Assignment 12. Update the data to include the price increases for a first class letter through January 2006 - when the price will become 39 cents. (Recent increases were 33 cents in 1997, 34 cents in 1999 and 37 cents in 2002.) Prepare a write-up and use your analysis to answer the questions a new:

· When will the cost of a first class postage stamp reach $1.00?

· When will the cost be 74 cents?

· How soon should we expect the next increase?

· In 1996, the analysis of stamp data historically seemed to show that the postage doubled every 10 years approximately. The cost in 2006 would seem to argue that pattern is no longer valid. Is there evidence to show a change in the growth pattern? Or, was the 'doubles every ten years' just a bad model?

My first attempt was graph the data. Then I thought that the curve might be close to a power or an exponential function. But just watching the scatter plot of the data, I cannot say if the curve follows either a power or an exponential function. However, using the coefficient of correlation (R²) between the variables maybe I can find how well the variables are related and then realize what curve is the best fit for the data.

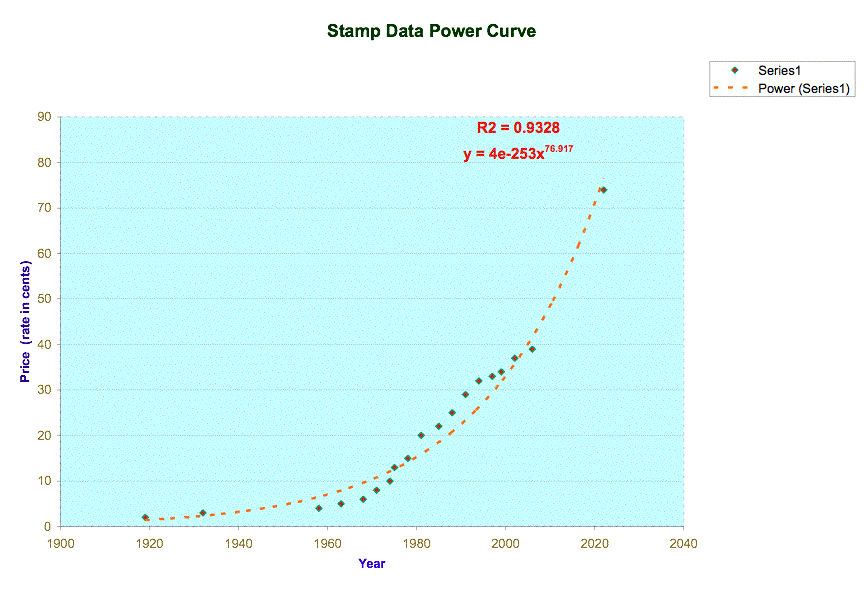
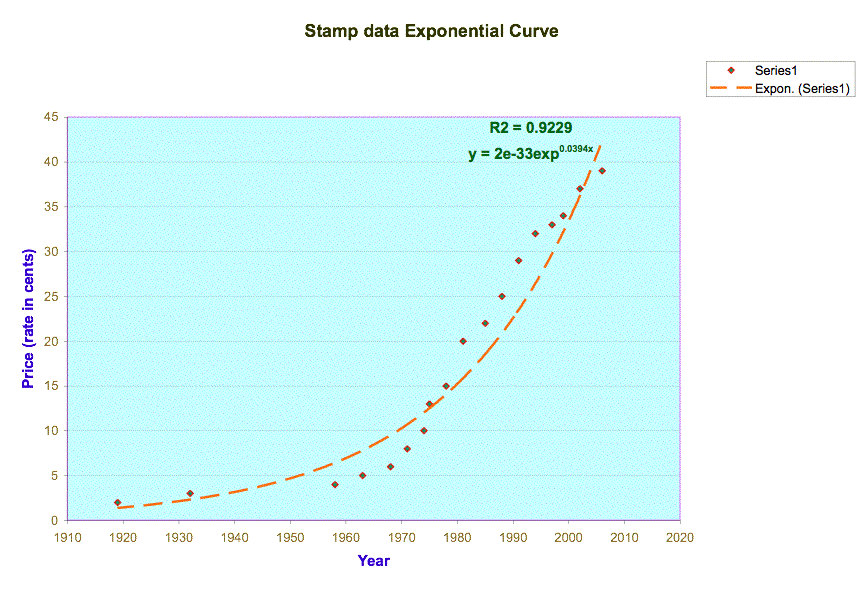
The coefficient of correlation values in both graphics are pretty close: 0.923 for exponential curve, and 0.933 for power curve. As the difference is not big enough, I think I can choose either one for predicting other values because both will be equally good predictors.

Let’s see how close are the outcomes using both equations in the following table:

x=Year	y=Price (rate in cents)	Exponential Function y=2E-33e^0.0394		Power Function y=4E-253*x^76.917
		Year Prediction	Price Prediction	Year Prediction	Price Prediction
1919	2	1919	1.4	1929	1.3
1932	3	1929	2.3	1939	2.2
1958	4	1936	6.4	1947	6.3
1963	5	1942	7.8	1952	7.6
1968	6	1947	9.5	1957	9.3
1971	8	1954	10.6	1964	10.5
1974	10	1959	12.0	1970	11.8
1975	13	1966	12.5	1977	12.2
1978	15	1970	14.0	1980	13.7
1981	20	1977	15.8	1988	15.4
1985	22	1979	18.5	1990	18.0
1988	25	1983	20.8	1993	20.2
1991	29	1986	23.4	1997	22.7
1994	32	1989	26.3	2000	25.5
1997	33	1990	29.7	2001	28.7
1999	34	1990	32.1	2001	31.0
2002	37	1993	36.1	2004	34.7
2006	39	1994	42.3	2005	40.5
2022	74	2010	79.4	2022	74.6
2029	100	2018	104.6	2030	97.3

I chose the power curve as predictor because is a little bigger. The equation for this curve is y = 4^-253 x^76.917, where x represents the year and y represents the price (rate in cents).

To know when the price will reach 1.00 dollar, we can replace y by 100 cents and then find the new value of x.

So, now 100 = 4^-253 ● x^76.917

x = (100 / 4^-253) ^76.917

and x = 2030. This means that the stamp will cost a dollar the year 2030. Of course, this is an approximate value.

The same can be done to find the year in which the stamp will cost 74 cents. So, now 74 = 4^-253 ● x^76.917

x = (74 / 4^-253) ^76.917

and x = 2022. This means that the stamp will cost 74 cents the year 2022. Remember that these values are approximate.

Are there significant differences if I use power function or exponential function? We can see in trhe next chart that the difference in price is very small between them (some cents) and some years were predicted exactly similar. The cells highlighted are the cells where there was any difference.

Table 1

Year	Price	Exponential Function		Power Function
		Prediction price using equation	Predictions year using equation	Prediction price using equation	Prediction year using equation
1919	2	1.37	1929	1.34	1929
1932	3	2.29	1939	2.25	1939
1958	4	6.38	1946	6.29	1947
1963	5	7.77	1952	7.65	1952
1968	6	9.46	1956	9.30	1957
1971	8	10.65	1964	10.46	1964
1974	10	11.98	1969	11.76	1970
1975	13	12.46	1976	12.22	1977
1978	15	14.03	1980	13.74	1980
1981	20	15.79	1987	15.44	1988
1985	22	18.48	1989	18.03	1990
1988	25	20.80	1993	20.25	1993
1991	29	23.41	1996	22.74	1997
1994	32	26.35	1999	25.53	2000
1997	33	29.66	2000	28.66	2001
1999	34	32.09	2000	30.95	2001
2002	37	36.11	2003	34.74	2004
2006	39	42.28	2004	40.50	2005
2022	74	79.41	2020	74.62	2022
2029	100	104.63	2028	97.34	2030

---

In 1996, the analysis of stamp data historically seemed to show that the postage doubled every 10 years approximately. The cost in 2006 would seem to argue that pattern is no longer valid. Is there evidence to show a change in the growth pattern? Or, was the 'doubles every ten years' just a bad model?

If we observe in the table 1, the price in 1981 was 20 and 10 years later in 1991 was 29. This fact suggests that the evidence does not show us that the postage price doubled every ten years. As a result the ‘doubles every ten years’ is not a good model.

Return to my Final Page