Problem1: Write parametric equations of a line segment through (7, 5) with slope of 3. Graph the line segment using your equations.

Before trying to solve this problem, let's investigate the following problem which might help us to solve this one.

Problem2: Graph x = t + 1 y = 2t - 1 for some appropriate range for t. Interpret. Is there anything to vary to help understand the graph?

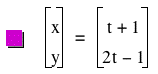
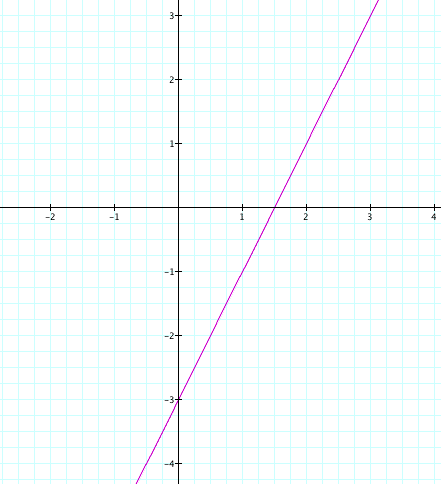
If we vary the coefficient of t in y = 2t - 1, both the slope of the line and the y-intercept change. If we don't change the coefficients of the t's but change 1 or -1 in the equations, it seems like the second line is parallel to the original line the only change being in its y-intercept.

You can click here to work on different equations.

If we try to write the equation of y depending on x, we see that y should be 2 times x plus something:

y = 2t - 1 = 2(t + 1) + a

2t - 1 = 2t + 2 + a then -1 = 2 + a then a = -3

So, y = 2x - 3

We can conclude that the ratio of the coefficient of t in the second equation to the ratio of t in the first equation determines the slope of the line.

So, going back to the first problem, parametric equations should look like:

x = at + b
y = 3at + d

Some more algebra will give us a relation between b and d:

y = 3x - 16

3at + 3b - 16 = 3at + d

3b - 16 = d

Now it is time to write the parametric equations. Let's choose a = 1 and b = 6. Then 3a = 3 and d = 5

x = t + 6
y = 3t + 2

And the graph looks like;