---

In this write-up I investigate the polar equation .

First, I set a = b = 1 and vary k through integer values.

For k = 0, the graph looks like

This makes sense because for k = 0, the equation becomes r = 1 + cos (0) = 2 and whatever the angle is r will be 2. So, the graph will be the set of points which are 2 units away from the origin.

And for k = 1, it looks like

Before going on with other graphs you can click here and onserve how the graph changes as k varies.

Here are the graphs for some other values of k:

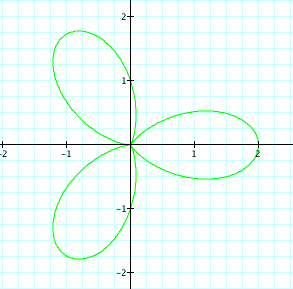
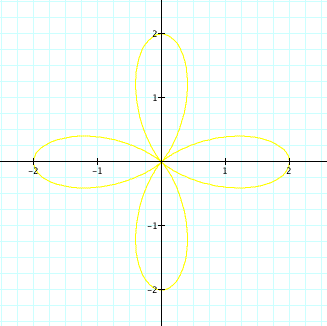
So, one thing that we can obseve and conjecture from these graphs is that k determines the number of leaves or the petals.

We observe another thing if we look at all the graphs in one picture:

The graph for k = 0, in other words the circle, seems to be the boundary for all others. Why?

This can be explained with a characteristic of the cosine function. Cosine of an angle will always be between -1 and 1. Since, it can't exceed 1, in our polar equation r won't exceed 2. So, none of the graphs will go beyond the circle.

Now, let's see what happens when k takes a negative value:

These look exactly the same as the previous graphs. Why? Again because of the cosine function. Cosine of an angle is equal to the cosine of the negative of the same angle.

Now, let's compare the graph of

with the graph of

.

For k = 0, the obvious is:

For k = 1:

Here, I wondered why the second one became a circle and I decided to play around withand see what it looks like as an equation in x and y.

The correspondance between polar corrdinates and the rectangular coordinates is like the following:

So,

Applying some trigonometric laws:

From here, we can see that

And, this is exactly the equation for the green circle!

Now, let's go back and compare our functions for other values of k:

So, a conjecture that we might have at this point is when k is odd graphs of the two functions have equal number of leaves and when k is even the graph of has twice as many number of leaves as the graph of .

Some other questions that could be explored:

Why do these functions behave the way they do? Why does k change the number of leaves?

What happens when a and b are also varied?

What happens when k takes non-integer values?

What happens if cosine function is replced with the sine function?