In this write-up I begin with an acute triangle ABC. Then I construct another triangle connceting the three midpoints of the original triangle. This is called the MEDIAL triangle. It is similar to the original triangle and one-fourth of its area. I construct G, H, and C for this new triangle. I compare to G, H, and C in the original triangle.

Conjecture1: The medial triangle has the same centroid as the original triangle ABC.

Proof: In the following figure two medians of ABC, namely AA' and BB', intersect two sides of A'B'C', namely C'B' and C'A', in points D and E respectively.

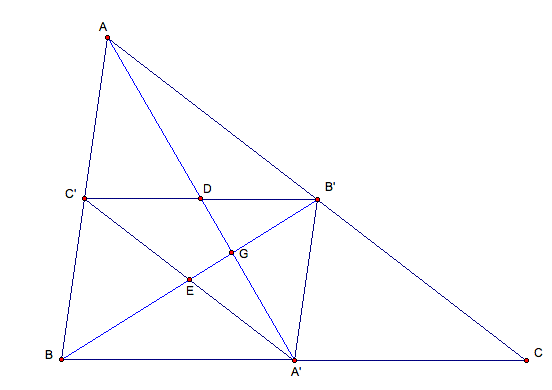
So, I need to show that D is the midpoint of C'B' and E is the midpoint of A'C'. I know that C'B' // BC and AC'/AB = 1/2. So, AC'D is similar to ABA' and C'D = BA'/2. Similarly, DB' = A'C/2. Since A' is the midpoint of BC, BA' = A'C. Hence C'D=DB' and D is the midpoint of C'B'. With a similar argument E is the midpoint of A'C'. Therefore, G which is the centroid of ABC, is also the centroid of A'B'C'.

Conjecture2: Circumcenter of the original triangle is the orthocenter of the medial triangle.

Proof: Draw two altitudes of A'B'C': C'I and A'F.

They intersect at the point O which is the orthocenter of A'B'C'. Since A'B' // AB, what is perpendicular to one is also perpendicular to the other. In this case, since C'I is perpendicular to A'B', it is also perpendicular to AB. Moreover, C' is the midpoint of AB. Hence, C'I is the perpendicular bisector of AB. Similarly, A'F is the perpendicular bisector of BC. As a result, O is the circumcenter of ABC.

Conjecture3: Euler segment of the medial triangle is half the length of the Euler segment of the original triangle. Click here to observe.

Proof: HGO form the Euler segment of ABC with HG = 2GO. Since orthocenter, centroid and the circumcenter of a triangle are collinear ­ forming the Euler segment ­ the circumcenter of the medial triangle should also be on the line formed by GO (There is only one line determined by two distinct points.). It is clear from the drawing that this point will be between H and G.

Let's assume that GO = 2x.

Now examine the following line segment:

HG = 2GO = 4x
NG = GO/2 = x
HN = HG ­ NG = 4x ­ x = 3x
NO = NG + GO = x + 2x = 3x

Hence, HN = NO.

So, N is the midpoint of HO and the Euler segment of the medial triangle is the half length of the Euler segment of the original triangle.