---

Question to be investigated: Construct a triangle and its medians. Construct a second triangle with the three sides having the lengths of the three medians from your first triangle. Find some relationship between the two triangles. (E.g., are they congruent? similar? have same area? same perimeter? ratio of areas? ratio or perimeters?) Prove whatever you find.

Before starting, it is important to note that we should construct the second triangle in such a way that changing the main triangle will change the second one and, hence we can observe some relationships. How to construct the second triangle in a way that will help us to see connections and prove them?

The construction will look like this:

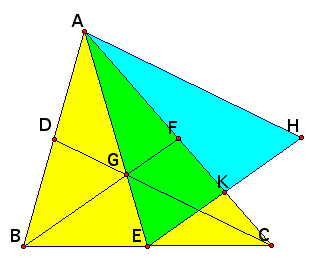
And, here is how it is constructed:

First draw the Triangle ABC and its medians. Then choose one of the medians AE as the base for the second triangle and draw a parallel line from the point A to DC and mark H such that |DC| = |AH|. Similarly, draw a parallel line from the point E to BF and mark H such that |BF| = |EH|. AEH is the triangle constructed from the medians of the triangle ABC.

Now, we can look for some relationships. Follow this link to observe how maipulating the given triangle influences the ratio of the area of the seond triangle to the area of the first triangle.

You will see that this ratio is constant and is equal to 3/4.

Here is the proof:

Let A(ABC) = 24x.

Then A(ABF) = 12x, since a median divides a triangle into two parts with equal areas.

We know that BG/GF = 2/1 because G is the centroid. So, A(AGF) = 12x/3 = 4x

We know that EH is parallel to BF and that E is the midpoint of BC, then K is the midpoint of FC.

So, AF/FK= 2/3 which means that A(AGF)/A(AEK) = (2/3)(2/3) = 4/9 = 4x/A(AEK) Hence, A(AEK)= 9x

Since, we have found that K is the midpoint of EH, we know that A(AEH) = 2 A(AEK) = 2(9x)=18x

Hence, A(AEK) / A(ABC) = 18x / 24x = 3/4

Observing the ratio of the perimeters, it seems like this ratio is between some constant values. Click here to make some observations. Working on triangle inequalities show that there actually are two such values.

First part: Apply triangle inequality to triangles ABG, BGC and CGA:

AG + BG >AB
BG + GC > BC
GC + AG > AC

Adding these three inequalities we find:

2AG + 2BG + 2 GC > AB + BC + CA
4/3 (AE + BF + CD) > AB + BC + CA
Hence, P (AEG) / P(ABC) > 3/4

For the second part, we need some construction:

Extend the given triangle in all three directions constructing parallelograms. It is easy to show that medians are also extended.

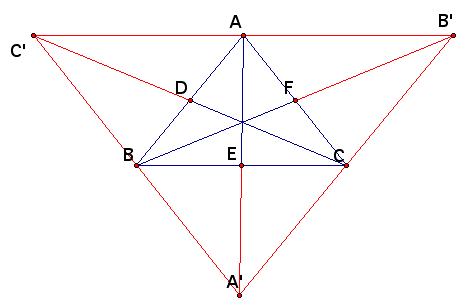
Here is what we can show using this figure:

CC' < AC' + AC

BB' < CB' + CB

AA' < BA' + BA

2(DC + BF + AE) < 2(AB + BC + AC)

P(AEG) / A(ABC) < 1

So, the final theorem is the ratios of the perimeter of the triangle constructed using the medians to the perimeter of the given triangle is greater than 3/4 and smaller than 1.