For this assignment I decided to investigate the following problem:

Find two linear functions f(x) and g(x) such that their product h(x) = f(x).g(x) is tangent to each of f(x) and g(x) at two distinct points.

First, I started with taking two linear functions randomly and observing their graphs and their product's graph. The only point was choosing functions with opposite slopes.
To be a little systematic I decided to start firth f(x) = ax + b g(x) = -ax + d

So, I chose f(x) = x + 2 and g(x) = -x + 1. Here is how the graphs look like:

It should be expected that since h(x) is the product of two linear functions with opposite slopes, it will be a parabola facing 'down'. However, for h(x) to be tangent to both f(x) and g(x) at two distinct points, its y-value at its maximum should be smaller that the y-value of the two functions' intersection point.

So, next time, to make use of symmetry, I worked with f(x) = ax + b, g(x) = -ax + b and chose b to be smaller than 1 so that b squared would be smaller than b. Here is the graph for f (x) = x + 7/10, g(x) = -x + 7/10 and h(x) = f(x).g(x) :

After a couple trials, I decided to have f(x) = x + 1/n and y = - x + 1/n and observe the graph as n changes. Click here to observe.

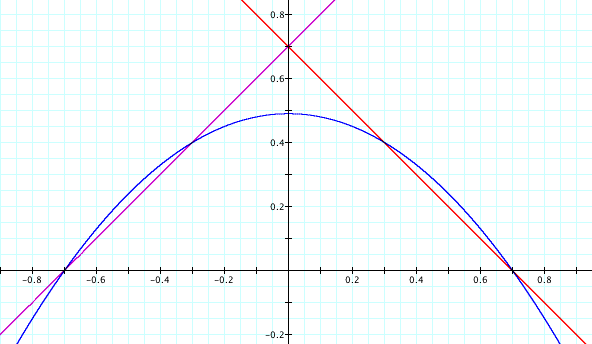
When I taught the parabola was tangent to both lines at two distinct points I stopped the animation and tried to see what functions looked like. As the following figure shows the y-intercepts of the linear functions seemed to be close to 1/2 so I decided to try f(x) = x + 1/2 and g(x) = - x + 1/2. And, it worked:

So, what is special about these functions? It seems like one has a positive slope whereas the other one has a negative slope, and the y-intercepts are the same.

However, the following functions don't work:

f(x) = x + 1/3 and g(x) = - x + 1/3

f(x) = 2x + 1/2 and g(x) = -x + 1/2

But, these work: f(x) = x + 1/3 and g(x) = -x + 2/3

Or f(x) = 2x + 1/3 and g(x) = -2x +2/3

So my final conjecture was: f(x) and g(x) should have slopes a and -a and y-intercepts adding to 1.

The geometrical observations led me to make some conjectures but the proof came from algebra:

Let f(x) = ax + b and g(x) = c(x) + d. Then h(x) = (ax + b)(cx + d)

For a line to be tangent to a parabola at only one point, the tangent drawn from the x-intercept of

the line to the parabola should have the slope of the line itself.

So, we need to take the first derivative of h(x) = acx2 + (ad + bc)x + bd which is h(x) = 2acx + (ad +bc)

f(x)= ax +b = 0 x = -b/a

h(-b/a) = a then ad - bc = a

Doing the similar operations with h(x) and g(x) gives -ad + bc = c

Hence a = -c.

Then inserting a = -c in ad - bc = a gives -cd - bc = -c dividing by -c (we can divide because slope can't be zero) gives b + d = 1