Assignment 2

Second Degree Equations

by Dorothy Evans

Let’s examine the equation

on the same axis using different values for d.

First let’s examine the parent function.

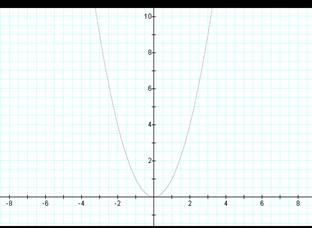
Notice the vertex lies on the origin (0, 0)

Now let’s see what the graph looks like when d from our original equation is 0.

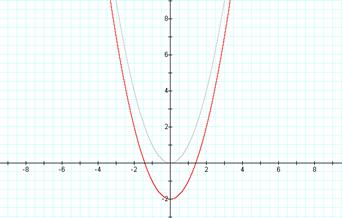
What do you notice about the graph of the equation compared to the parent graph?

Q: Did every point on the graph move or did the graph stretch down?

You should notice the vertex of the parent graph has moved down 2 to the point (0,-2).

Now let’s see what happens when we make d = 2

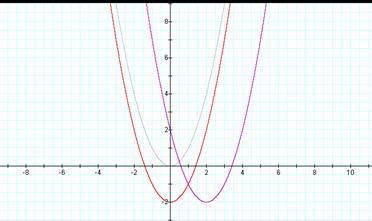
What happened in the new graph (purple)?

The graph moved right 2

So what do you think will happen if d = 6?

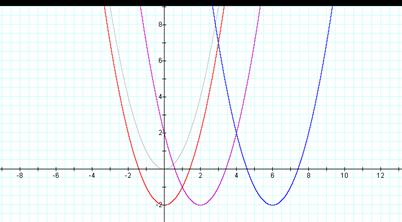
That’s right the vertex moved right 6 spaces to (-2, 6)

What would happen if we made d = -4?

Can you guess?

Scroll down to see

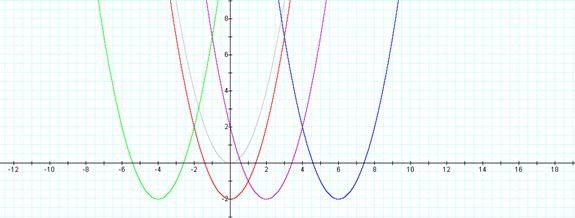
Conclusion

Can you make any conjectures from this demonstration about how a change in d in the equation affects the graph?

What would you conjecture? Test your hypothesis on another graph such as