Graphs
by Dorothy Evans
Starting with the
equation 
Observe the graph of this equation.
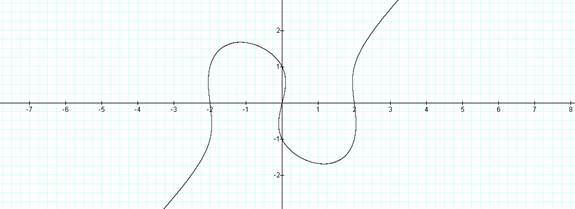
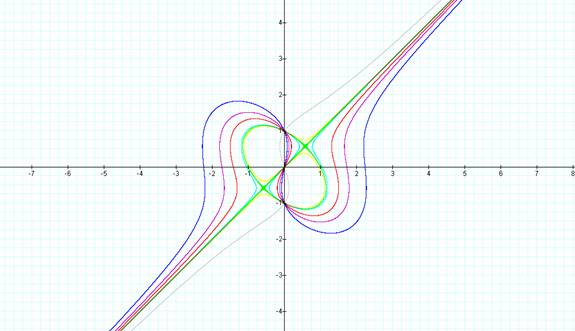
See how the graph changes (below) when replacing the 4 in the equation above with the numbers 5, 3, 2, 1, 1.1, 0.9, -3. Notice that as the number decreases the wavy line centered at the origin gets smaller and smaller until an elliptical shape is formed. Another interesting phenomenon is that all functions intersect at the points (0,1) and (0,-1) as well as the origin (0,0).
Questions to ponder: Is the elliptical shape in the green graph a real ellipse or does it just look like one? How would we test this? Do the lines really touch in the elliptical like shape or are they just so close that they appear to touch but don’t actually touch?
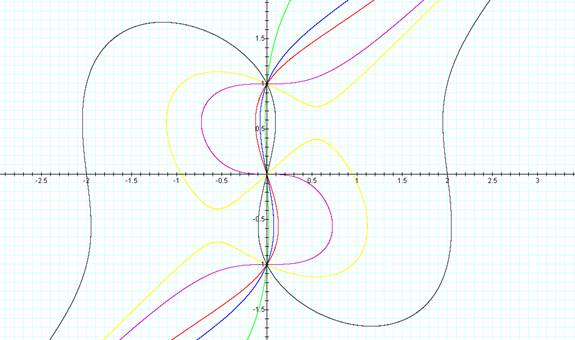
To see the phenomena when the 4 in the original equation is a negative number let’s look at the original graph and five values where the 4 is replaced with .9, 0, -3, -5 and -20.
Original graph.
Notice that all of these graphs (above) also share the origin (0,0), (0,1) and (0,-1). Of particular note the purple graph where the 4 was replaced with a 0 appears to have the same shape as the original graph inverted across y=x.
Questions to ponder: If you changed the number 4 from the original equation to the numbers from -1 to 1 you would observe similar shaped graphs (at a smaller scale) to those when the 4 is interchanged with integer values?
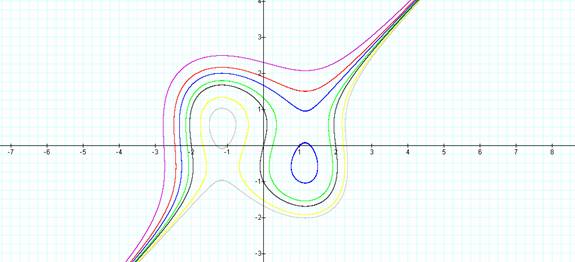
Next we look at what happens when a constant is added to one side of the equation.
Original
equation
Notice the graphs no longer share the points (0,0), (0,1) and (0,-1) and they are not symmetrical about any linear equation
Also notice egg shapes are formed when on each side of the axis when adding and subtracting 3 from the left side of the equation.
Question to ponder: Is the egg shape symmetrical? If it is symmetrical what x coordinate is it symmetrical about? If it’s not symmetrical does a value exist where it is symmetrical and what would be that value? How would we find it?