Assignment 3: Quadratic Equations by Dorothy Evans

Let’s examine the equation and look at its roots.

First we will graph the equation as and examine its roots (i.e. where y=0)

Let’s see what happens as we change b.

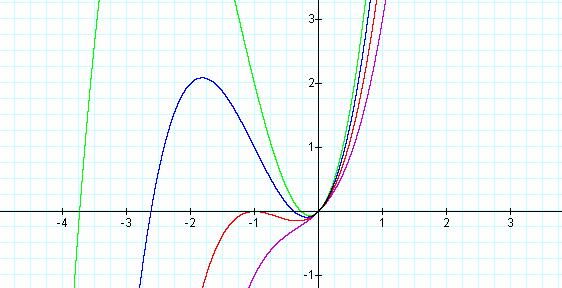
It seems clear that for b=1 there is only 1 root at (0,0)

What about for where b=2, it looks like there are two roots one at (0,0) and one at (-1,0). Can we prove it?

Let’s look for a minute where the graph came from

What would happen if we factored the equation?

Next we would get

Then we utilize our product property to get either

or

Further factoring we know that we can factoragain to get

so

is a root.

What about our next equation where b=3?

This one doesn’t look so simple. It’s somewhere between -3 and -2 but how can we find out where.

Let’s see what we can do to solve it.

Starting with set y=0

We again factor to get

Then we know x=0, but how do we factor ?

We could do 2 different things, first we could complete the square to solve or we could use the quadratic formula.

Utilizing the quadratic formula we get .

Does this answer seem reasonable? We can estimate and get x=-.38 and x=-2.62.

So what would the general equation be for the roots?

It would appear we could plug in b for b and solve.

So

Let’s factor

Next we get x=0 and x=

So does this tell us anything about the local maximum we see on the left side of the graph.

Can we now hypothesize about the value of that local maximum?

What would you guess?