Assignment 8: Altitudes and Orthocenters

By Dorothy Evans

For this write up I chose #13.

13. The internal angle bisectors of triangle ABC are extended to meet the circumcircle at points L, M, and N, respectively. Find the angles of triangle LMN in terms of the angles A, B, and C. Does your result hold only for acute triangles?

I chose this investigation specifically because I didn’t remember any specifics in class and wanted to find the answer to the question. My first step was to duplicate the triangles and circumcircle and measure the angles of the triangles. My first conjecture was that the angles would be proportional to each other. After some simple calculations in GSP it became quite obvious that this was not the case.

However it seems intuitively obvious that there would be a relationship between the angles since the red triangle is constructed from the black triangle. I then conjectured that the angle measurements may be the average of the other two angle measurements. (i.e. mÚABC = (mÚNLM + mÚMNL)/2. An example of this demonstration (not a proof) is included below.

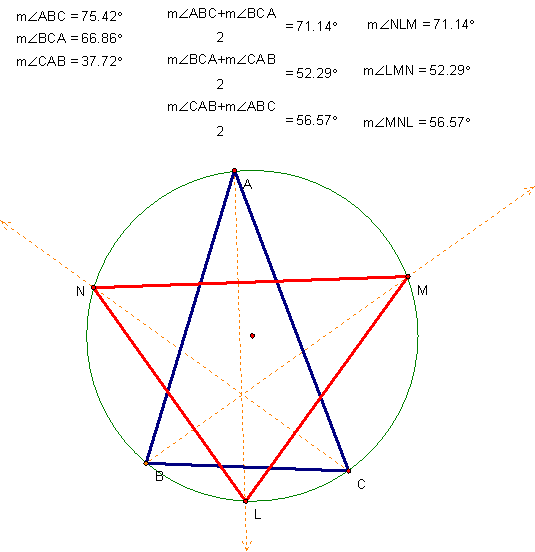
To see this GSP file for yourself click here.

In investigating the main question I animated each of the points A, B, and C and observed the relationship between the angles of +ABC and +LMN. From this it appears that the relationship holds true for acute and obtuse +ABC.

Of further note I found it interesting that no matter what the shape of +ABC, +LMN was always acute.

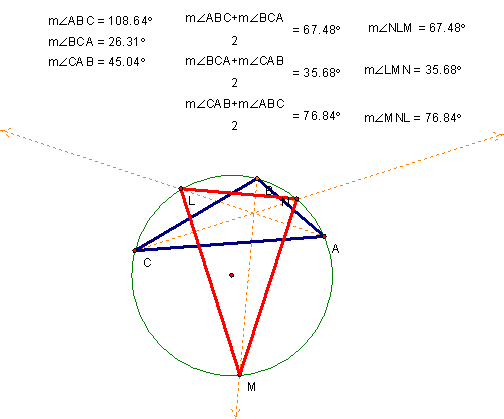
To see this GSP file click here.