Pedal Triangles

By Dorothy Evans

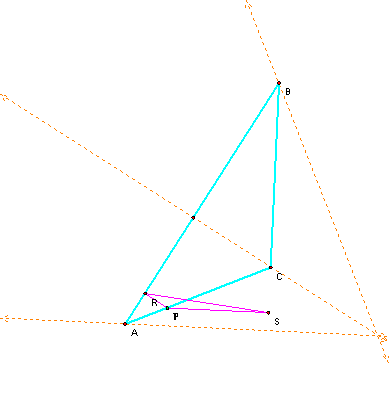
Let triangle ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) locate three points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.

I found this investigation to be one of the most interesting since the Pedal Point P can be anywhere on the plane of ABC. After creating the Pedal Point and Pedal Triangle I chose to write up my investigation of #7 and found a relationship between the when the Pedal Point P is on a side of a triangle and the orthocenter.

First let’s look in general what happens as P moved to the side of the triangle ABC.

I first noticed that as P moved towards the sides of +ABC the point P would move towards a vertex of +RST. Click here to try it on your own.

While this is interesting, it also seems an obvious phenomenon since the pedal point is constructed from the perpendicular lines through point P to the sides of +ABC.

Next I decided to see what would happen if I merged the pedal point P onto a side of +ABC and animate point P along that side of the triangle. Here you can see I have merged Point P onto segment AC.

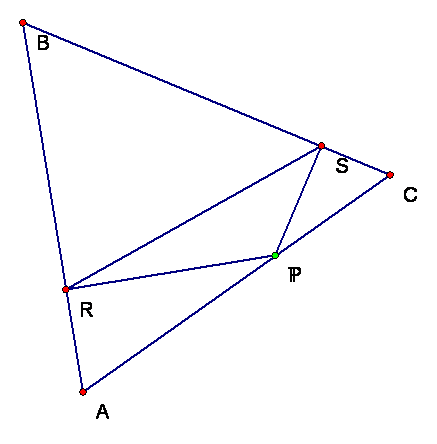
Notice that as P moves from the vertex A to the vertex at C the vertices R and S will slide up and down the sides of +ABC for only a part of the segment.

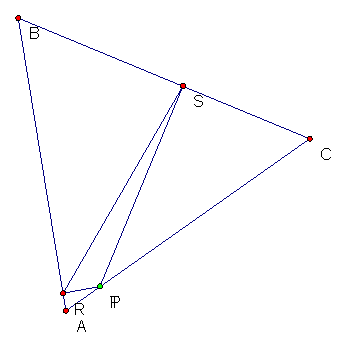
Here I traced the point R and S as they moved up and down while P was animated on the segment AC. This led me to question what would happen if +ABC were obtuse and is there a relationship between the movement of R and S in relationship to +ABC. To see P animated along segment AC click here.

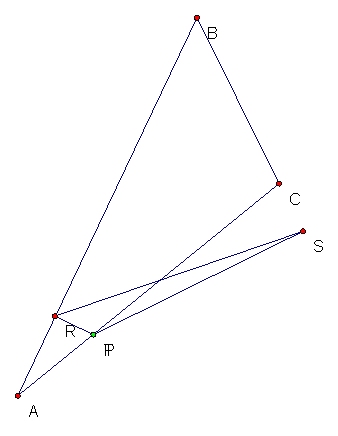
Then I made +ABC obtuse to see what the traces would look like for point S and R. (See above)

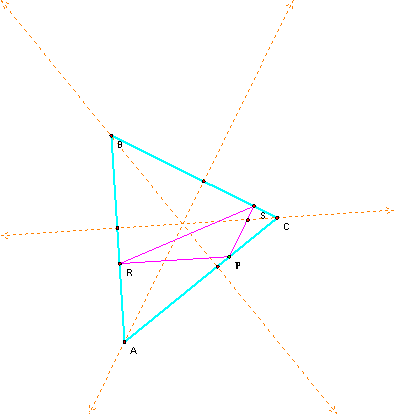
Next I conjectured that there may be a relationship between the traces and one of the triangle centers. My first try I created the centroid of +ABC but could not find a relationship between the traces and the centroid. Next, I tried the orthocenter since it is constructed from the perpendiculars through each vertex to the opposing side of the triangle. Here I found a relationship between the orthocenter and the Pedal Point P when it’s on a side of the triangle.

Here is the acute +ABC. Here is the obtuse +ABC.

Notice for both of these (the acute and obtuse) as the pedal point P moves along the side of the triangle. The other two vertices of the pedal triangle (R and S) move along the segment between the vertices of +ABC and where the altitude intersects on the other side of +ABC. To see the animation click here.

Furthermore in answer to question 8. What if P is one of the vertices of triangle ABC? In this case the pedal triangle collapses into a line.