
Polar Equations
By
Jeffrey R. Frye
This investigation looks at the “n-leaf rose”. I started by exploring the results when different variables were changed in the equation below.
![]()
The values of a and b were held constant and equal, as the value of k was changed. The illustrations indicate that the number of “leaves” in the rose is determined by the value of k. The length of the “leaves” becomes larger as the value of a and b are increased. An example of this is shown in the picture below.
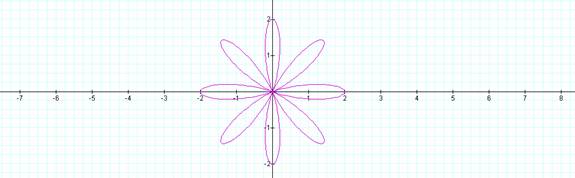
An interesting observation occurs when the values of a and b are changed to different values. When a < b, another set of leaves is shown. When the value of k is odd the second set of leaves is smaller and inside the larger set. When the value of k is even, the second set of leaves is smaller and between the larger leaves.
Explore this observation using Graphing Calculator.
A comparison observation was made by replacing the above relationship with those listed below.
![]()
The same observation from above was seen with this equation. When k is odd the number of leaves is the same as k. When k is even the number of leaves is 2k. As the value of b is increased, the length of the leaves is increased. The orientation of the leaves does not change if k is a negative integer.

Explore this observation using Graphing Calculator.
![]()
These same observations appear to hold true for the sin as they did for the cos.
Changing to sin does rotate
the rose.
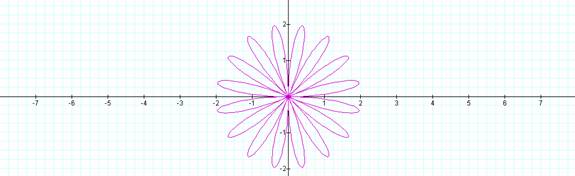
Explore this observation using Graphing Calculator.
Return to main page