Triangle Centers Write-up

By

Jeffrey Frye

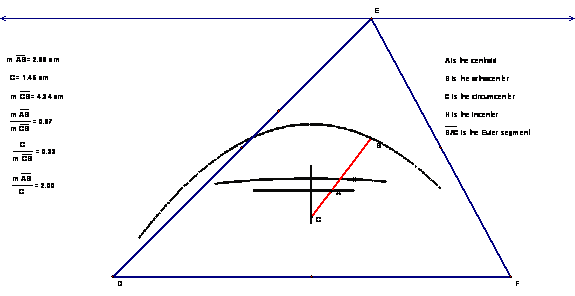
Construction of triangle centers in this investigation will explore the centroid, circumcenter, orthocenter, and incenter of a triangle. It will also look at the relationship between these constructions. One relationship is the Euler segment. The Euler segment connects the circumcenter, centroid, and orthocenter in this order in triangles. The relationship is that the centroid is located between the circumcenter and orthocenter, and is 2 times the distance from the orthocenter as from the circumcenter. The incenter is not on this segment except when all of the segment lengths are maximized. When these points are traced by moving the triangle vertex along a line parallel to its opposite side, the trace of the orthocenter is an arc through the other vertices, the centroid tracks parallel to the side, and the circumcenter traces perpendicular to the side. The incenter tracks on an arc, and remains between the centroid and the orthocenter. At the maximum, the perpendicular track is coincident with the Euler segment and the incenter. The graphic display is shown in the illustration.

To do your own exploration using Geometer’s Sketchpad, click here.

Return to Main Page.