Tiling Pools Learning Task

This task is similar to the introductory tiling learning task in that students will continue to familiarize themselves with developing algebraic expressions to model problems in context. The context for this task is swimming pools. Students will examine various pool designs and use their explorations to develop algebraic expressions to model the area of the swimming pool(s).

1. In the figures below, there are diagrams of swimming pools that have been divided into two sections. Swimming pools are often divided so that different sections are used for different purposes such as swimming laps, diving, area for small children, etc.

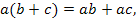
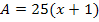
a) For each pool, write two different but equivalent expressions for the total area.

Students should already be familiar with the properties of the area of a parallelogram, i.e., that . The lengths of each of the rectangular pools are separated into two sections. Therefore, the students must realize that the total lengths will be the sum of each of the sections.

Pool #1: The area of the first pool is equal to its length (x + 1) times its width (25), yielding an algebraic expression of its area. An equivalent expression can be determined by using the distributive property. The equivalent expression for the area of pool #1 is 25 + 25x.

Pool #2: The area of the second pool is equal to its length (22 + x) times its width (x), yielding an algebraic expression (22 + x) ∙ x of its area. Once again, the equivalent expression is obtained by distributing, obtaining a total area of

b) Explain how these diagrams and expressions illustrate the Distributive Property.

In order to obtain the equivalent expressions for the area of pools 1 and 2, the Distributive Property of multiplication had to be used. The definition of this property states that and two equivalent expressions (as denoted by the equal sign) are produced. For example, for Pool #1, we found that or depending on how the student(s) defined the length and width. In either case, we used the Distributive Property, which tells us that 25(x + 1) is equivalent to

. We used the same procedure to calculate the equivalent expression for Pool #2.

_____________________________________________________________________________________________________________________________________________________________________________________________________________

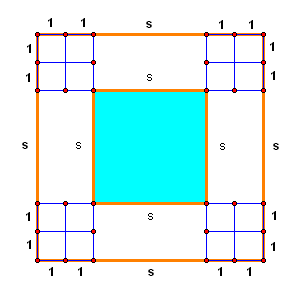
In-ground pools are usually surrounded by a waterproof surface such as concrete. Many homeowners have tile borders installed around the outside edges of their pools to make their pool area more attractive. Superior Pools specializes in custom pools for residential customers and often gets orders for square pools of different sizes. The diagram at the right shows a pool that is 8 feet on each side and is surrounded by two rows of square tiles. Superior Pools uses square tiles that are one foot on each side for all of its tile borders.

The manager at Superior Pools is responsible for each job and needs an equation for calculating the number of tiles needed for a square pool depending on the size of the pool. Let N represent the total number of tiles needed when the length of a side of the square pool is s feet and the border is two tiles wide.

Students should realize that the only thing that remains constant in this problem is the dimensions of the border since this information was given to us in the problem statement, i.e., each border tile is 1’x1’. Also, the students need to remember that these pools are square pools. This is an important clue as to how to determine the length and width of the pool.

Although there are multiple ways to solve this problem, modeling the situation using a picture will help most students visualize the scenario in order to address questions regarding dimension.

2. Write a formula in terms of the variable s that can be used to calculate N.

Many of the students will most likely attempt to draw the complete picture of the pool, including the entire outside border, in hopes that they can count the border tiles one-by-one. This is not necessary if the students realize that the most important areas of the pool border are the four outside corners of dimension 2’x2’ (see the above diagram). The other sections need not be included in the calculation because we already know that these pieces are equal to side s.

Also, although it does not specifically ask the students to use area in their calculations, they must be able to see that the only way to calculate the number of tiles needed to create the border of the pool is by subtracting the area of the pool from the area of the entire outside square that is created by the border. What is left will be the area of the border. Since each of the border tiles are 1’x1’, the area of the border will also equal the number of tiles, N, needed to create the border. See the calculations below to obtain N.

Length of the pool = s

Width of the pool = s

Length of the pool w/border = s+4 (2 + 2 + s + 2 + 2)

Width of the pool w/border = s+4 (2 + 2 + s + 2 + 2)

Width of the pool w/border = s+4

Area of the pool =

Area of the pool with the included border =

Area of the border = Area of the pool with the included border – Area of the pool

= 8s + 16 = N

It is important to note that there are many possible answers that the students could come up with depending on how they modeled the scenario. Some of these possible answers include:

3. Write a different but equivalent formula that can be used to calculate N.

The students should see that both terms of their expression have 8 in common. Therefore, by factoring out an 8 from each term and writing the result, the students will have created an equivalent expression for N.

Again, the equivalent expressions will vary depending on how the students modeled the scenario.

4. Give a geometric explanation of why the two different expressions in your formulas for the number of border tiles are equivalent expressions. Include diagrams.

The student in the above example found the two equivalent expressions to be . Ironically enough, this student used the fact that the area of the border is the same as the number of tiles needed along the border due to the fact that each tile’s dimension was 1’x1’. By understanding that it was an area problem and coming up with his expression from the above diagram, he, in turn, gave a geometric explanation of his expression. To make things interesting, let’s say that another student came up with the same set of expressions but came up with them in a different way. How would this student represent the scenario geometrically?

Let’s look at the second student’s diagram…

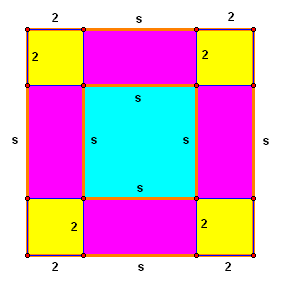
tiling pools 4.bmp

This student recognized that the entire border was comprised of 8 shapes, 4 squares of dimension 2’x2’ and four rectangles of dimension 2’x s’. This can be translated into the following expression: . This student also realized that, due to the dimensionality of each border tile being 1x1, the area of the border is the same as the number of tiles, N, needed to create the border.

The most important thing in any of the examples that students come up with is that they are able to explain their reasoning and connect the expression to the figure!!

5. Use the Commutative, Associative and/or Distributive properties to show that your expressions for the number of border tiles are equivalent.

Students should be familiar with the above mentioned properties. But, for the sake of being clear, here are the basic property definitions that students should already be familiar with by this point.

Commutative Property of Multiplication and Addition: and

Associative Property of Multiplication and Addition: and

Distributive Property:

Let’s revisit the different possibilities that some of the students could come up with for expressions for the number of border tiles, N.

Using as our starting point, let’s see if we can get the other expressions to equal this one.

: The distributive property tells us that this expression is equivalent to .

: The distributive property tells us that this expression is equivalent to

: Expanding this expression gives .

· If asked how to proceed at this point, many students will respond that they need to “FOIL” the product in order to combine like terms. This is a great opportunity to show the kids that “FOILING” as they may or may not know it, is just a fancy way of learning how to distribute a product of two binomials.

By distributing the s and the 4 of the first factor to the s and the 4 of the second, you will simplify the above expression to . By combining like terms, a further simplification yields . Note: The Commutative Property tells us that !

: The distributive property tells us that Combining like terms gives the equivalent expression .

: The distributive property tells us that . Furthermore, by applying the Commutative Property, we know that .

: The distributive property tells us that . Combining like terms gives 8s+16.

: The distributive property tells us that Combining like terms gives

By the transitive property, since every expression is equivalent to every expression is equivalent to each other!

The next exercises in this task require that the student is fully comfortable with the concepts, procedures and solutions of the first 1-5 parts of the task. For those students who are still having difficulties with any of the skills in parts 1-5, refer them to the supplemental text based on individual student need.

6. How many 1-foot square border tiles are needed to put a two-tile-wide border around a pool that is 12 feet wide and 30 feet long?

This is a very similar problem to the above. However, instead of a square pool, the pool is now rectangular. Modeling the scenario using a picture or diagram is still a great way for the kids to get a visual grasp of what is going on and what is being asked.

As in the above problems involving the square pool, the number of 1-foot square border tiles needed to put a two foot wide border around the a 12’x30’ rectangular pool is found by taking the area of the outer rectangle (formed by the outer edge of the border) and subtracting the area of the pool.

Using the same diagram, you can also calculate the number of tiles needed to form the border by looking at the shapes that comprise the pool border. A student could look at the geometry in one of two ways:

(1) two rectangles of dimension 2’x32’ and two rectangles of dimension 2’x14’:

(2) four squares of dimension 2’x2’, two rectangles of dimension 2’x12’ and two rectangles of dimension 2’x30’:

In all three scenarios, the student should find that the number of tiles needed to form the 2-foot-wide border around the rectangular pool is 184 tiles.

7. Write an equation for finding the number N of border tiles needed to put a two-tile wide border around a pool that is L feet long and W feet wide. Explain, with diagrams, how you found your expression.