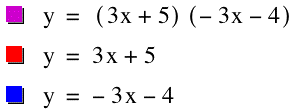Investigation of the product of
linear functions
by
Kristy Hawkins
Find two linear functions
f(x) and g(x) such that their product
h(x) = f(x).g(x)
is tangent to each of f(x)
and g(x) at two distinct points. Discuss and illustrate he method
and the results.
Let f(x) = ax+b and g(x)
= cx+d
We know that for linear
function to be tangent to h(x) then the slope of h(x) must be
equal to that function.
Clearly the slope of f(x)
= a and the slope of g(x) = c, since they are both linear equations.
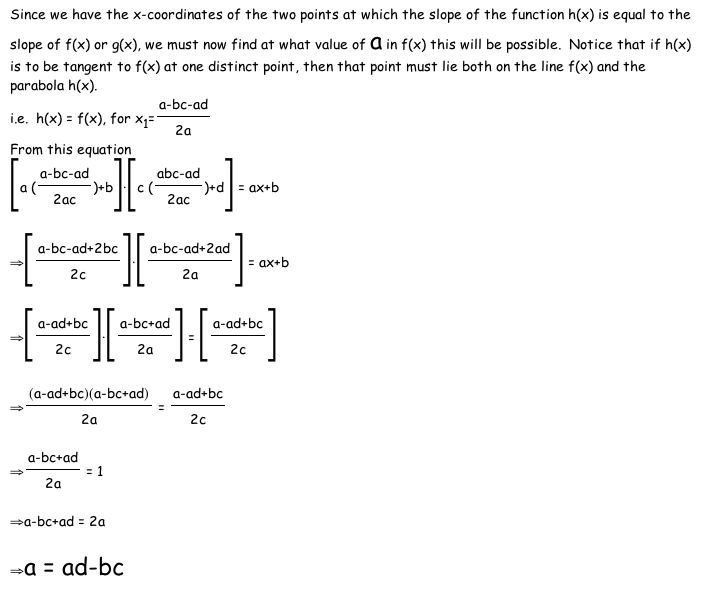
In order to find the arbitrary
equations f(x) and g(x) for which this relationship holds true,
we will solve h'(x) = a and h'(x) = c. This will perhaps give
us some relationships that we can use to define any linear functions
for which this relationship will hold true.
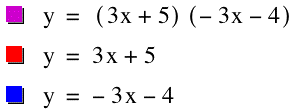
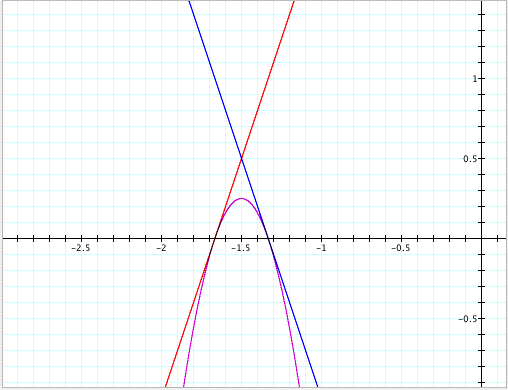
Wow! This f(x)
and g(x) are tangent to their product at 2 distinct points.
But we also know
how to find ANY function for which this is true by using our derived
equations. To generalize our equations we will write:
where a does not
equal 0
Here is a GSP
file to demonstrate all of the possible functions for which this
is true. Click here!
Click on the button in the top left
hand corner of the file marked a to see what happens when a is varried. Then press
it again to make the variable stop. Do the same for both b and x.
It is interesting so see that varying
the value of a will
change the shape of the parabola, while varying the value of b only moves it side to side.
Why to you think this is so?
Return