Comparison of Parametric Curves

by Kristy Hawkins

 

A parametric curve in the plane is a pair of functions

x= f(t)

y= g(t)

where the two continous functions define ordered pairs (x, y). The two equations are uually called the parametric equations of a curve.

 

We will now investigate two parametric equations of a curve and compare them as certain variables change. Our parametric curve is,

Which looks like this curve when a=1, b=1, and t is between 0 and 2 pi. Hmmm, isn't that the unit circle? Think about this for a minute. When we think about the unit circle, each point on that circle has the coordinates (cos(t), sin(t)). This is exactley what our parametric curve is defining when a = b = 1.

Let's look at what our curve will look like when we change the values of a and b. First let's look at what happens as a and b both get larger.

So we see that as a and b get larger at the same rate, then our parametric curve expands outwards. For each integer that a and b increase, a new circle is added with a radius equal to that of the previous parametric curve plus one. This makes us wonder what it would look like to vary a and b from zero to some other positive integer. Take a look at this animation to see what happens.

 

As we see in this animation, our parametric curve continues to grow toward a circle with infinite radius as a and b get larger. What would happen if we try the same exploration as a and b get smaller?

So now we see that the parametric curve when a = b= 1 is the same as when a = b = -1. Actually, the curves when the values are integers are also the same. What happens for ALL negative numbers?

Click here to see the animation.

Did you find that these two explorations lead to the same parametric curves?

What is the curve when a < b?

What would you guess that is would look like? Let's explore!

Let's first keep 'a' constant at one and make 'b' larger.

 

 

 

 

 

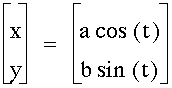
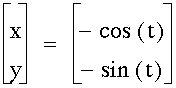
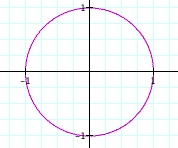
<----- a=1, b increases

We see that as b increases, our circle seems to be smushed into an ellipse. It is very interesting that it seems to be stretched out more the higher b becomes. If we think about these curves in terms of their coordinates, the x-coordinate will always be just cos(t) like on our unit circle. But as we increase b, our y-coordinate increases, causing the orginal unit circle to stretch out.

 

 

 

 

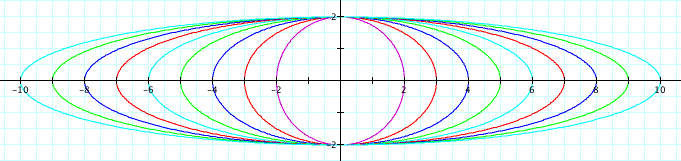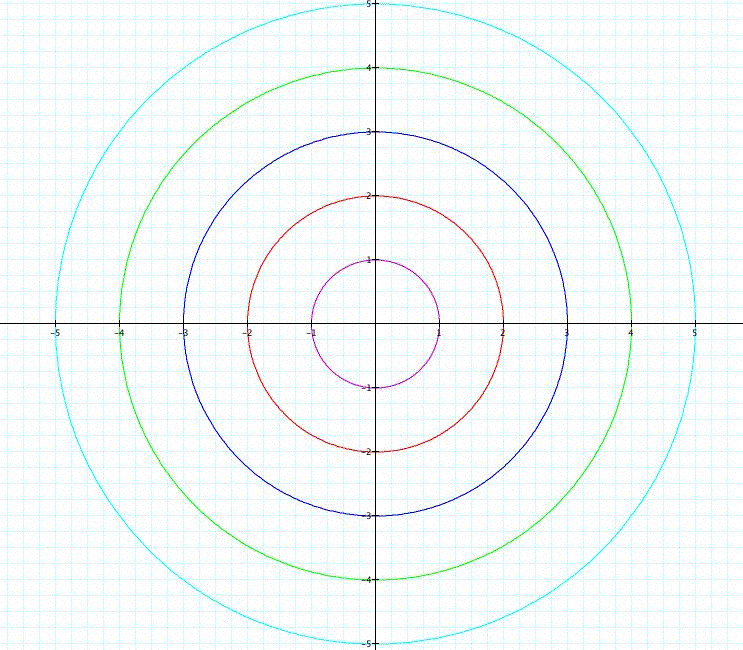
What do you think will happen when b is held constant and a increases?

 
 In this illustration, b is held constant at two while a increases. We see the same thing happening now that we did before, except for now the y-coordinate stays the same wile the x-coordinate stretches out. Think about this in the same way that we though about the unit circle.

 

Return