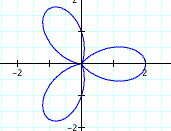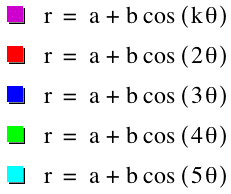Investigating Polar Equations
by Kristy Hawkins
What is a polar equation? It is an equation for a curve
written in polar coordinates. But what are polar coordinates?
They are a way to describe the location of a point on a plane.
A point is given coordinates
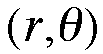 where r is the distance from the point to the origin
and theta is the angle measured counterclockwise from the polar
axis to the segment connecting the point to the origin.
Let's investigate one of these polar equations.
where r is the distance from the point to the origin
and theta is the angle measured counterclockwise from the polar
axis to the segment connecting the point to the origin.
Let's investigate one of these polar equations.
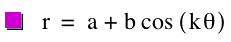
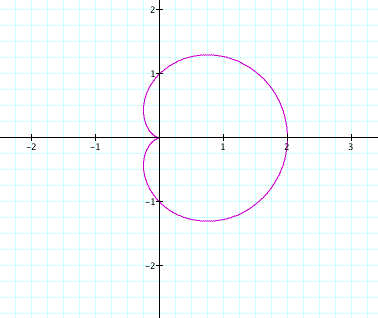 This picture here shows our equation when a=b=k=1.
I wonder what will happen as we change these coefficients...Let's
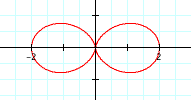
try keeping a=b=1, but varying k to different integer values.
k=2,3,4
This picture here shows our equation when a=b=k=1.
I wonder what will happen as we change these coefficients...Let's
try keeping a=b=1, but varying k to different integer values.
k=2,3,4
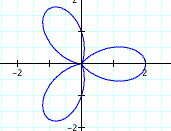
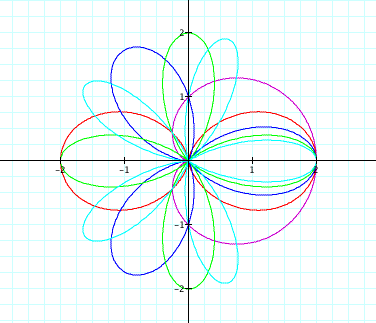
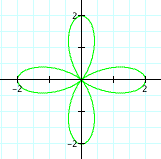 So it looks like for each positive integer increase
of k, we get a new petal on our flower.
Look at how the petals form when k varies from zero
to ten.
What happens when k is negative? Open this Graphing
Calculator file to find out!
Another interesting investigation would be to see what
happens when a is not equal to b. First let's try a<b for integer
values. What do you think it will look like?
So it looks like for each positive integer increase
of k, we get a new petal on our flower.
Look at how the petals form when k varies from zero
to ten.
What happens when k is negative? Open this Graphing
Calculator file to find out!
Another interesting investigation would be to see what
happens when a is not equal to b. First let's try a<b for integer
values. What do you think it will look like?
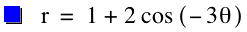
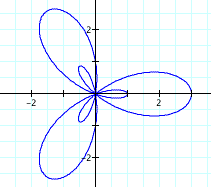 Wow, this looks like one petal inside each of the 3
petals. This happens for each integer value of k. What would happen
if we keep increasing b? Explore.
Here are some more interesting situations to investigate
as well:
Animation of b varying
from 0 to 10.
Animation of a varying from 0 to
10.
Wow, this looks like one petal inside each of the 3
petals. This happens for each integer value of k. What would happen
if we keep increasing b? Explore.
Here are some more interesting situations to investigate
as well:
Animation of b varying
from 0 to 10.
Animation of a varying from 0 to
10.
Return