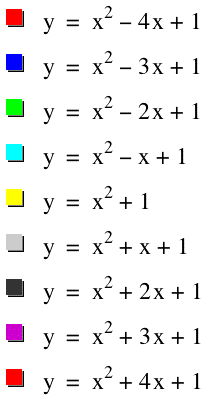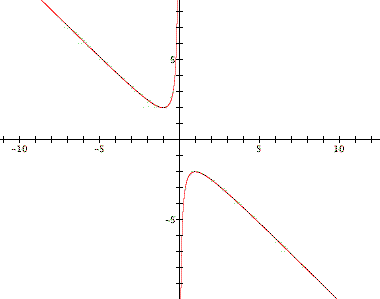Investigation
of Quadratic Equations
by
Kristy Hawkins
The standard form of a quadratic
equation is
To begin investigating this
equations, I will set two of the variables a, b, and c as constant
while varying the other one. This will show us what happens to
the graph as the one variable changes. Let us first hold a and
c as constants and vary b. What will happen?
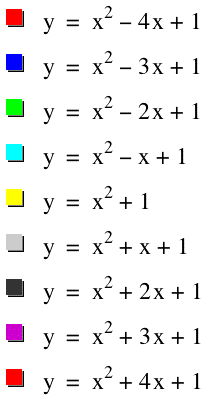
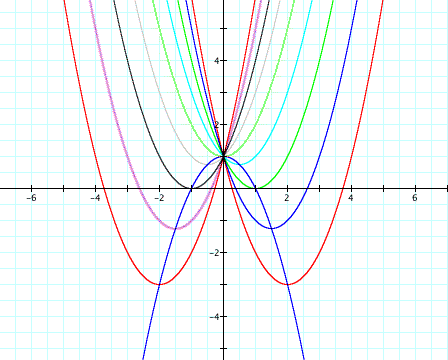
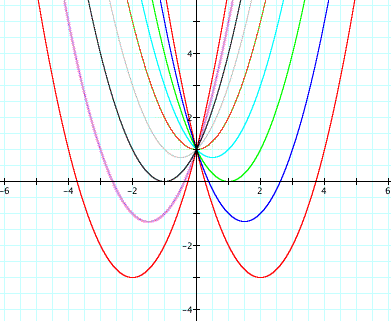What happens to the parabola
as b changes from -4 all the way to 4? They all seem to have the
same shape and the same y-intercept at (0,1). But what is changing?
The position of the parabola is changing as well as the roots.
If we look closely we can see that from (-2,2) there are no roots,
while at -2 and 2, there is a double root (This can also be seen
by looking at the equation at these points and noticing that they
are perfect squares). Along with this observation, we see that
there are 2 roots when b=-4, -3, 3, and 4. This would lead us
to assume that as b approaches infinity in both directions from
2, there will always be two real roots.
How can we describe the
way that these parabolas' shift as b varies? Let's look at the
locus of the vertices of these parabolas. If we can find an equation
that will describe this locus, then we will have a way to talk
about how the parabola shifts.
We can show that this locus
is
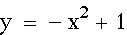This shouldn't be too hard.
We know that the y-intercept must be at 1 because every parabola
that we have looked at passes through that point. This locus must
also pass through (-1,0) and (1,0) which will be it's roots. We
also know that this new parabola must have a negative orientation.
Putting all of these facts together gives us our formula, and
our illustration below.
Now, what would these graphs
look like in the xb-plane?
Consider the equation
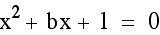If we decide to graph this
relation in the xb plane we will get the following graph.
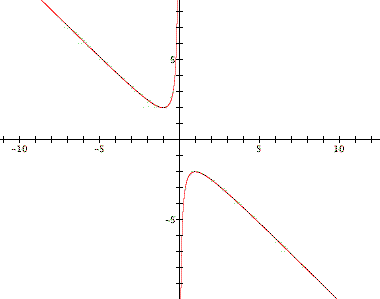If we take any particular
value of b, say b=3, and overlay this equation on the graph we
add a line parallel to the x-axis. If it intersects the curve
in the xb plane the intersection points correspond to the roots
of the original equation for that value of b. Why?
So here we hve a different
view of our roots than before, which can be very helpful when
investigating our quadratic equations.
Try this one yourself. Fix
b and c while varying c.
Return