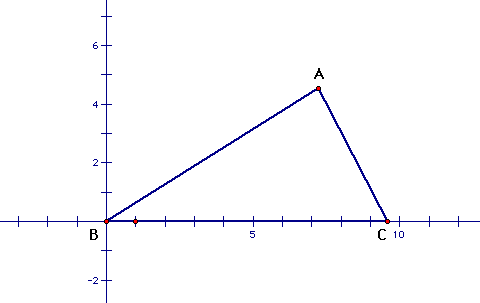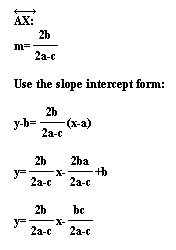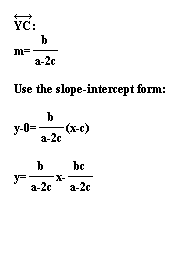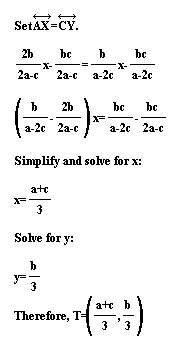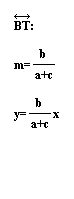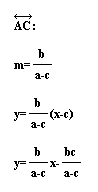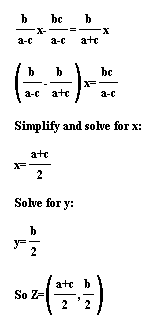Triangle Proofs

Do they meet?

Kristy Hawkins

So often we know the statements of theorems pertaining to the geometry of triangles, but we have never explored why they are true by proving them. In my experience, I have often take statements to be true without really knowing why they are. Over the years, my understanding of the benefits of the proofs of mathematical theorems has expanded enormously, which has encouraged me to approach these proofs that are seen here.

What about those Angle Bisectors?

We have all heard that the three angle bisectors ofthe internal angles of a triangle meet at a point called the incenter. How do we know that these three lines intersect at the same point?

Here we will prove that the three angle bisectors of the internal angles of a triangle are concurrent.

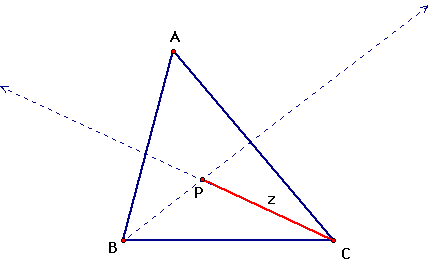
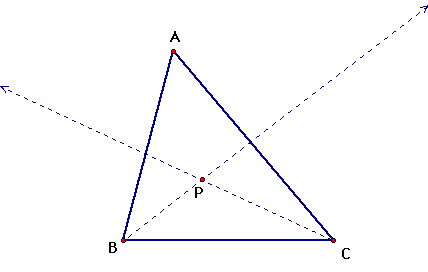Consider the arbitrary triangle ABC, in which the dotted lines are bisectors of the angles B and C and P is the intersection of these angle bisectors.

Denote CP=z

Since z bisects <ACB, the <ACP is congruent to <BCP by the definition of an angle bisector.

Denote<BCP = c1 and <ACP = c2.

Drop the perpendicular segments from P to all three sides of triangle ABC. These are the green segments.

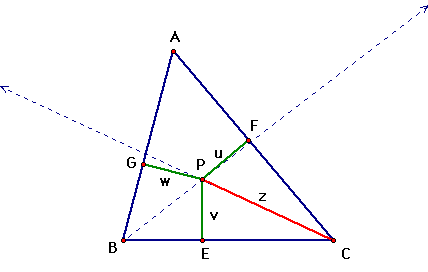Since triangles PFC and PEC are right triangles,

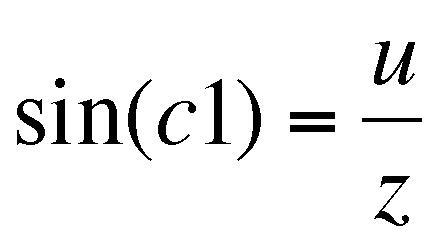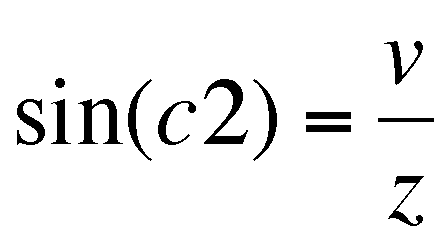Since c1=c2 as said before, then we see that u=v.

We can make the same argument with right triangles GPB and EPB to show that w=v. Therefore, u=v=w. This means the perpendicualr segments from P to the three sides of our triangle are all congruent. At the end of our proof, we will show what special circle the three points G, F, and E lie on. Can you make a guess now?

Now we will draw the segment from A to P. We must show that this segment bisects angle BAC to show that the angle bisectors of the three internal angles of a triangle are concurrent.

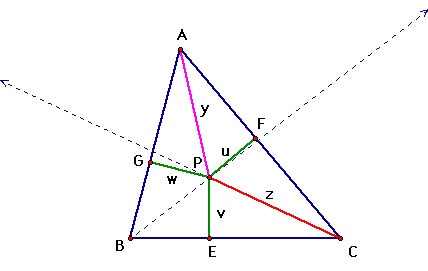Let <BAP=b1 and <CAP=b2. We have already shown that u=w which makes one pair of sides of the triangle congruent, and we see that they both share the side y. Since triangles APG and APF are right triangles and we have shown two sides to be congruent, then GA must equal FA. This would mean that these two triangles are congruent and therefore all of their angles are congruent making b1=b2.

This means that AP is the angle bisector of the vertex A and all three angle bisectors are concurrent!

P is called the incenter of the triangle ABC. This point is the center of the incircle of which G, F, and E are the points where the incircle is tangent to the triangle.

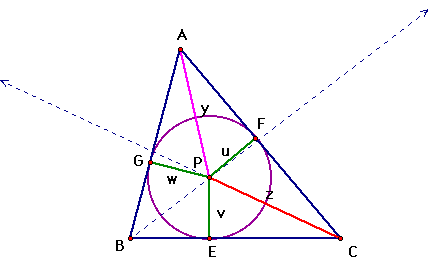Click here to play with a dynamic GSP file of the illustration of this proof.

A Deeper Look at the Medians

We have also heard that the intersection of the three medians of a triangle is called the centroid. How do we know that these three medians intersect at the same exact point?

Here we will prove that the three medians of a triangle are concurrent

and

that the point of concurrence, called the centroid, is two-thirds the distance from each vertex to the opposite side.

For this proof we will place and arbitrary triangle into the coordinate system and use our algebra skills to prove each part of the proof.

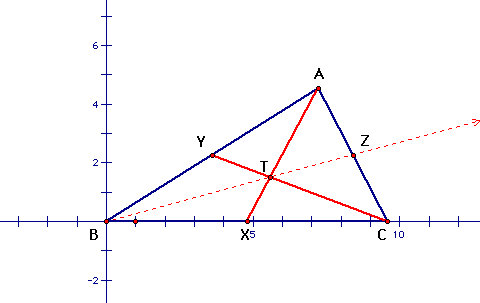
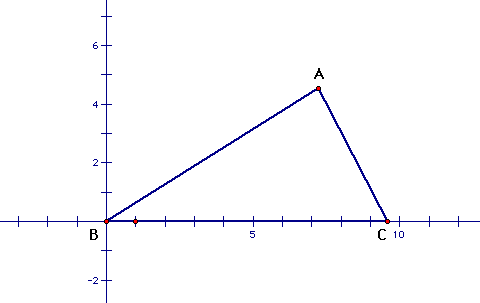Let AX and CY be medians of our triangle. (This means X is the midpoint of BC and Y is the midpoint of AB.) Also let their intersection be T.

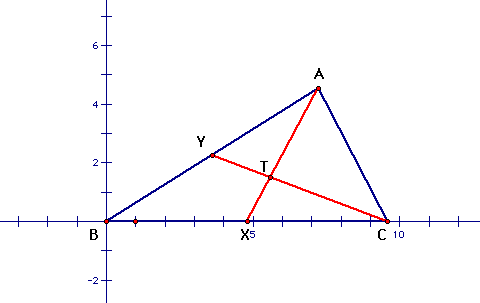We must prove that the line BT intersectsthe segment AC at the midpoint of AC, which we will call Z.

Let's look at some algebra to find the equations of the line passing through A and X and the line passing through Y and C so that we can calculate their intersection.

We must first find the coordinates of X and Y.

It is clear that X=(c/2, 0). By similar triangles, Y=(a/2, b/2). These points will help us calculate our lines.

Now since T is the intersection of these two lines,

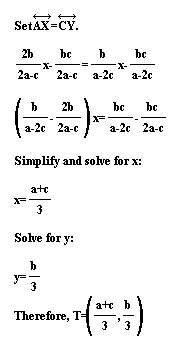Now that we have the coordinates of T, we can calculate the equation of the line passing through B and T and the line passing through A and C in order to help us find the coordinates of point Z. If we can prove that Z is the midpoint of AC, then we will be able to conclude that all three medians pass through one point and that point is T.

Now we can set these two equations equal to each other and solve for Z.

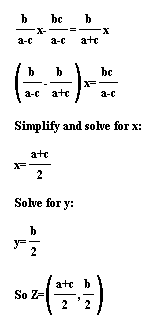Since b/2 is the midpoint of AC (shown by similar triangles), line BT intersects segment AC at the midpoint of AC, which is Z.

Conclusion: Since AX and CY are the medians of triangle ABC which intersect at T and BT intersects AC at it's midpoint, then all three medians of triangle ABC pass through the common point T, which is called the centroid.

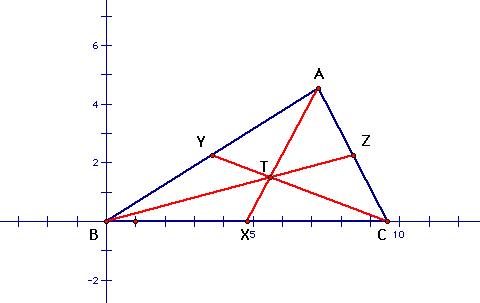Both of these proofs have shown us that given an arbitrary triangle, the three angle bisectors meet at the incenter and the three medians meet at the centroid.

Return