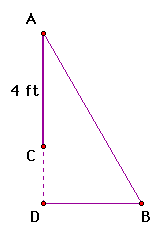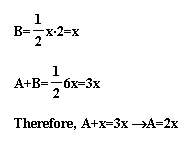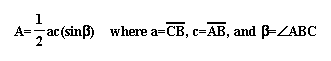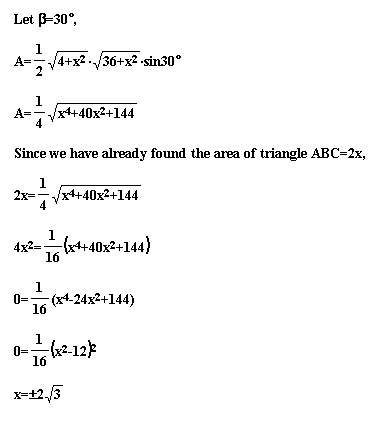Viewing Art
by
Kristy Hawkins
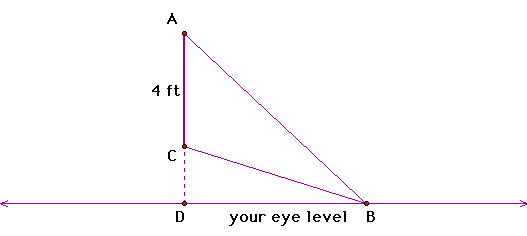
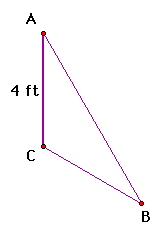
A 4 by 4 picture hangs on a wall such that its bottom
edge is 2 ft above your eye level. How far back from the picture
should you stand, directly in front of the picture, in order to
view the picture under the maximum angle?
Side view:
To begin solving this problem, we can look at what
happens to the angle as you would start far back and walk closer.
Click here to play with the GSP file.
You notice that as you will approach the painting from
far away, the angle initially becomes larger until a certain point.
At that point, forward motion causes the angle to decrease as
it will finally arrive at zero if you were touching the wall underneath
the painting. GSP Animation
If we investigate this sketch and measure angle ABC,
we see by moving B along the eye level the angle measure is never
greater than 30 degrees. For this investigation, lets assume that
the maximum angle is 30 degrees from what we observe. If this
is so, what is the disantce from the wall to where you are standing?
We can use the area of the 3 different triangles to
find this distance, let's call it x. But first, we have to find
the hypotenuses!!
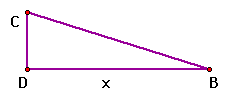Since triangle BCD is a right triangle, we can use
the Pythagorean Theorem to show:
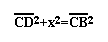
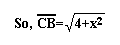
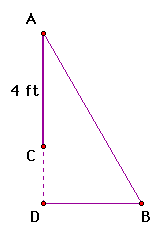We will look at triangle ABD in the same way to find
the hypotenuse AB.
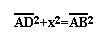
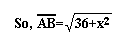Now that we have both hypotenuses, we can begin to
look at the area of the triangles. It is easy to see that the
area of triangle ADB consists of the sum of the areas of triangle
BCD and ABC. Maybe this will come in handy, or maybe not, but
it is still good to notice as we are investigating this problem.
Let's call the area of trianlge ABC=A, the area of
triangle CBC=B, so the area of trianlge ABC=A+B
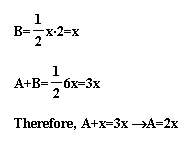There are two ways to find the area of a triangle.
The most well-known way is A=(1/2)basexheight, but there is another
formula that might help us.
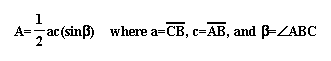
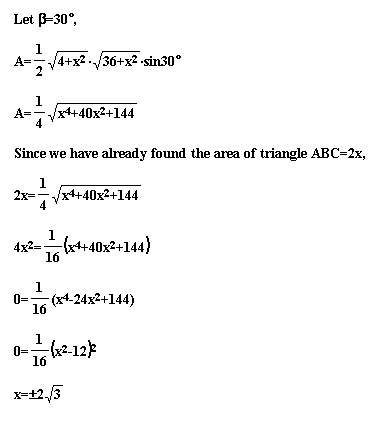This bit of algebra shows us how far away from the
painting, x, that a person must stand to make the viewing angle
equal to 30 degrees. This distance is approximately 3.464 feet.
Return